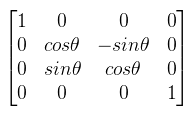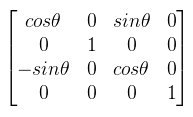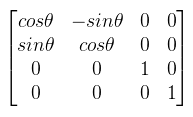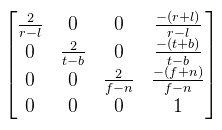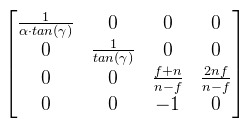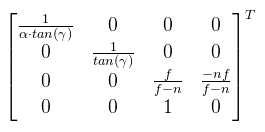|
Az időnként előforduló elméleti jellegű diskurzusok és fejtegetések közben feltűnt, hogy némelyek megijednek a cikkekben elvétve fellelhető matekos részektől, pedig semmi olyat nem szoktam írni, amit ne tudna megérteni egy óvodából frissen kirúgott
gyagyás. Azonban láthatóan igény van egy olyan cikkre ami elmagyarázza legalább az olyan alapvető fogalmakat, mint például az Lp normával értelmezett korlátoslineáris funkcionál (hehehe).
Tartalomjegyzék
Gyorstalpaló matematikai jelölésekből.
Természetesen a legtöbbnek a konkrét magyarázata lentebb olvasható. A billentyűzet limitációi miatt nem tudok mindent megkülönböztetni, úgyhogy a hasonló jeöléseket ne tessék félreérteni. A jegyzethez képest eltérő jelöléseket *-al jelöltem, azt sem kéretik félreérteni. Középiskolában azt tanultad, hogy a vektor egy irányított szakasz, aminek van kezdőpontja és végpontja. Ez az amit most elfelejthetsz. Mivel azonos hosszú és irányítású vektorokat egyenlőnek tekintünk, elég őket
helyvektorként megadni (tehát a kezdőpontja az origó, és a végpontját adod meg). Nyilván minden két ponttal megadott vektor konvertálható ilyenbe úgy, hogy a végpontból kivonod a kezdőpontot.
Ami még fontos (és tulajdonképpen ezzel kellett volna kezdeni), az a Descartes szorzat fogalma, ami két halmazon értendő, és a két halmaz elemeiből alkotott rendezett párok halmazát jelenti: Ilyetén módon a kétdimenziós vektorok halmaza R × R, a háromdimenziósaké R × R × R, stb. Ezeket röviden R2, R3, stb.-nek jelöljük és meglepő módon minden n természetes számra Rn és Cn (mostantól Kn) vektortér. Továbbra is pongyolán: a V vektortér egy W (nem üres) részhalmazát a V alterének nevezzük, ha W maga
is vektorteret alkot a V-beli műveletekre (melyeket fent olyan jól bemutattam). Fontos, hogy a műveletek eredménye nem mutathat ki az altérből (ha fent nem lett volna világos), tehát nem minden
részhalmaz altér.
vektort az a1, ..., ak vektorok lineáris kombinációjának nevezzük. Továbbmenve, azt mondjuk, hogy az a1, ..., ak vektorok lineárisan függetlenek, ha abból, hogy következik, hogy λ1 = ... = λk = 0. Ha tehát a lineáris kombináció nulla, de valamelyik lambda nem nulla, akkor a vektorok nem függetlenek (hanem összefüggőek). Az összefüggőség tipikusan azt jelenti, hogy valamelyik vektor előáll a többi lineáris kombinációjával (szélsőséges esetben egy másik vektortól csak hosszban különbözik). Most jöjjön egy fontos fogalom: a b1, ..., bk vektorokat a V vektortér bázisának hívjuk, ha lineárisan függetlenek, és minden V-beli vektor előáll ezek lineáris kombinációjaként. A vektortér dimenziója a benne levő tetszőleges bázis elemszáma (ami furcsa módon Kn-re mindig n). Néhány következményt illik megemlíteni, például hogy egy n dimenziós vektortérben bármely n + 1 vektor lineárisan összefüggő (különben bázis lenne), illetve egy W altér dimenziója legfeljebb ugyanannyi lehet, mint V dimenziója (például a háromdimenziós térnek egy altere a kétdimenziós tér). Továbbá ha b1, ..., bn bázis, akkor persze a definíció alapján minden vektor előáll ezek lineáris kombinációjával, de az is igaz, hogy ez az előállítás egyértelmű. Tehát egy tetszőleges x ∈ V vektor felírható alakban. A lamdákból összerakott (λ1, ..., λn)T oszlopvektort az x vektor b1, ..., bn bázisra vonatkozó koordináta oszlopának hívják. A T ne zavarjon meg senkit, ez azt próbálja jelezni, hogy egymás alá kéne írnom az értékeket (innen az oszlopvektor), de ezt nyilván nem tudom most megtenni. Sőt, ha b1, ..., bn az úgynevezett kanonikus bázis (pl. R3-ban (1, 0, 0)T, (0, 1, 0)T, (0, 0, 1)T), akkor a lamdbák értelemszerűen egybeesnek x elemeivel. 3D grafikában a leggyakrabban használt művelet az, amikor két bázis között transzformálunk pontokat. Ehhez meg kell mondani, hogy a két bázis közötti kapcsolat hogyan írható le.
Legyen a kiinduló bázis e1, ..., en, a célbázis pedig 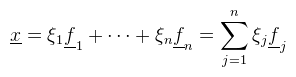 de persze az fj bázisvektorok előállnak az ei bázisvektorokkal (a bázis definíciója alapján): 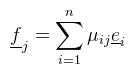 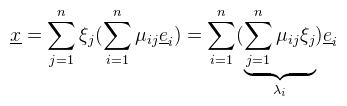 és ezzel felírtuk x-et az eredeti bázisban. Az elvégzett átalakítások minden további nélkül megtehetőek, a vektortér definíciója alapján (és mivel T test). Értelmezzük először, hogy mi történik, illetve miért jelöltem meg λi-vel a belső szummát. Az alapfeladat az alábbi:
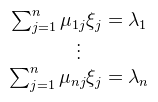 Most fogjuk ezeket a μij-ket és írjuk fel őket egy táblázatba: 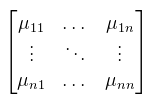 és nevezzük el ezt a szerencsétlent (n-edrendű négyzetes) mátrixnak. Pongyolán mondva oszlopvektorok egymás mellé pakolásáról van szó. Különösen fontos ez, mivel programozáskor sosem szoktunk bázisokkal bíbelődni, hanem ezt a mátrixot adjuk csak meg. Ezzel a jelöléssel felvértezve pakoljuk az ei bázist az E-vel jelölt mátrixba, az fi bázist pedig az F mátrixba. A fenti μij-s mátrixot jelöljük A-val, ekkor a bázisok közti váltást röviden írhatjuk le: F = EA (és nem fordítva!). Ezt fogom majd mátrixszorzásnak hívni (később). Hasonló meggondolásokkal a megoldandó lineáris egyenletrendszer pedig Ax = b alakban írható (ez nem a fenti x). Természetesen nem csak négyzetes mátrixok léteznek, sőt a mátrixokkal könyveket lehetne megtölteni, amit én itt nyilván nem fogok megtenni, de a lényeges dolgokat felépítem a későbbi bekezdésekben.
Középiskolában voltak ilyen fogalmak, hogy skaláris szorzat, vektoriális szorzat, stb. Ezeket én is bevezetem, de nem az ott tanult definícióval, ugyanis annál sokkal drámaibban is meg lehet ezeket fogalmazni.
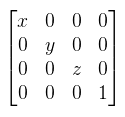
Rn-ben a skaláris szorzás a következőképpen definiálható: Tehát a vektorok megfelelő elemeit összeszorzod, majd a szorzatokat összeadod. Középiskolában a definíció úgy hangzott, hogy <a, b> = |a| |b| cos γ ahol γ a két vektor által bezárt szög. Mivel ott a vektornak más értelmezése volt, nem használható a fenti képlet, csak némi meggondolással. Ennek ellenére ez egy igen fontos egyenlőség, ugyanis ha a két vektor normalizált (a hosszuk 1), akkor a skaláris szorzat megadja a közbezárt szög koszinuszát. Vegyük most a |.|: V → R függvényt, amit definiáljunk a következőképpen: és nevezzük el az x vektor hoszzának. Megjegyezném, hogy (Rn, |.|) egy úgynevezett normált tér (sőt Banach tér), a |.| függvény pedig egy norma, sőt neve is van: euklideszi norma (mily meglepő). De menjünk tovább a mátrixokkal. Természetesen mátrixokat is lehet összeadni (ugyanúgy mint vektorokat), de elég ritkán használatos, így nem is pazarlok rá több szót. Egy gyakrabban használt művelet a skalárral való szorzás, ami szintén ugyanaz mint vektoroknál, tehát a mátrix minden komponensét megszorzod a skalárral. Most jön egy nem túl meglepő dolog: a mátrixok vektorteret alkotnak ezen két műveletre. Ha nem lett volna még elég a fontos dolgokból, akkor most jön a következő legfontosabb dolog: a mátrixsszorzás. A fentiekből már lehet sejteni, hogy ez nem komponensenként történik meg, hanem "skaláris szorzatokkal". Az A és B mátrix szorzatát AB-nek írjuk, ennek elemeit a következőképpen lehet kiszámolni: 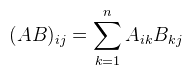 Tehát az A mátrix i-edik sorát "skalárisan szorozzuk" a B mátrix j-edik oszlopával. Papíron ezt úgy lehet ezt jól leírni, hogy az A mátrix jobb felső sarkához illeszted a B mátrix bal alsó sarkát, az eredményt pedig alá számolod ki. Nem lehet elégszer hangsúlyozni, hogy nem kommutatív, viszont asszociatív. Az A mátrix főátlóját alkotják azok az Aij elemek, ahol i = j (vagyis bal felső sarokból jobb alsó sarokba). Az A mátrix transzponáltjának nevezzük és AT-vel jelöljük azt a mátrixot, amit úgy kapunk, hogy az A elemeit tükrözzük a főátlójára. 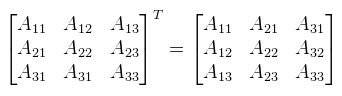 Nyilván ha most egy C = AB mátrixszorzatot veszünk, akkor az írható úgy is, hogy C = (BTAT)T. Persze ez semmin nem változtat, viszont ebből is lászik, hogy baromira nem mindegy hogy melyik oldalról szorzol egy mátrixxal! A DirectX ezt az utóbbi "jobbról szorzok" szemléletet használja, míg az OpenGL (és egyébként minden matematikai irodalom) az eredeti balról szorzást. Kiemelném, hogy mind a kettő helyes, amíg konzisztensen mindig csak az egyiket használod. Ha elkezded kavarni őket, akkor vicces dolgokat fogsz tapasztalni. Egy további fontos fogalom ami a szorzáshoz kapcsolódik a mátrix inverze (a szorzásra nézve). Ahhoz, hogy ezt értelmezni lehessen be kell vezetni egy egységelemet (jelöljük ezt I-vel és legyen a neve egységmátrix), amire teljesül, hogy IA = AI = A. Legyen I az a mátrix, melynek főátlójában 1-esek vannak, mindenhol máshol 0. Ekkor az inverz az alábbi egyenlőséggel értelmezhető: A-1A = AA-1 = I. Szintén egy gyakran használt fogalom, viszont nem minden mátrixnak van inverze (később lesz róla szó). A bekezdés végén még nézzünk meg néhány fontos azonosságot (a vektorok oszlopvektorként értendők):
Ezeket jó észben tartani, mert sokat kell használni. A vektoriális szorzatot nem említem most meg, majd egy későbbi bekezdésben (ugyanis nem egy általános művelet). Szöveges feladatokat nem találtam, úgyhogy most mindenki elképzeli, hogy az alábbi egyenletrendszer valami nagyon fontos dolognak a formalizálása.
x - y + 3z = 2 3x - 6y - z = 25 Persze ezt egy általános iskolás is meg tudná oldani úgy, hogy mondjuk kifejezi x-et a második egyenletből aztán behelyettesíti az elsőbe és kifejezi y-t, stb. Ha viszont adnék neki egy 30 ismeretlenes egyenletrendszert, akkor valószínűleg kapitulálna (hacsak nem lelkiismeretes). Ha esetleg még azt is megoldaná, akkor kerítenék egy neki való egymillió ismeretlenes operációkutatási feladatot, csak hogy legyen dolga (a mai fiataloknak úgyis túl sok szabadideje van). Mivel mi lineáris algebrát tanulunk, ezért okosabbak vagyunk és ismerjük a Gauss elimináció nevű módszert, ami ráadásul könnyen algoritmizálható, így tetszőlegesen rövid időn belül lekörözzük a kölyköt (akár még fogadhatunk is vele). Ha jobban megnézzük az egyenletrendszert, akkor valójában egy mátrix-vektor szorzás van bal oldalon, tehát Ax = b alakban írható, ahol x = (x, y, z)T, b = (-9, 2, 25)T és A pedig az együtthatókból készített mátrix. A megoldáshoz húzunk egy vidám vonalat, a bal oldalára írjuk a mátrixot, a jobb oldalára pedig b-t. 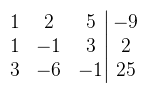
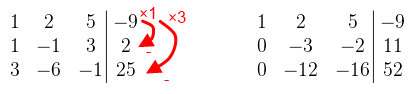 Ahol 0 van az jó. A főátlóban mindegy, hogy mi van, amíg nem nulla. A következő elem amit eliminálni kellene az a -12. Az első sort nem használhatod, mert akkor elrontja a 0-t, tehát akkor a második sor -4-szeresét adjuk hozzá a harmadik sorhoz. 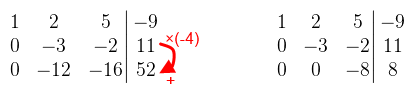 A harmadik sor már tök jó, osszuk le -8-al, hogy könnyebb legyen számolni. Folytassuk az eliminálást: a harmadik sor kétszeresét adjuk hozzá a második sorhoz, a -5-szörösét pedig az elsőhöz. 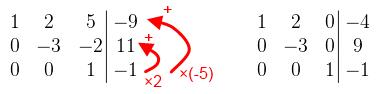 A második sor is majdnem jó lett, leoszthatjuk -3-al, és már csak a 2-t kell eliminálni. A második sor kétszeresét vonjuk le az elsőből. 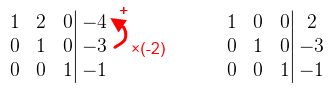 És a megoldás x = 2, y = -3, z = -1. Látható, hogy szisztematikusan haladtam, először a főátló alatt, aztán fölötte. Néhány dolgot viszont észben kell tartani:
Mondok egy még jobb hírt: egy mátrix inverzét ugyanezzel a módszerrel ki lehet számolni. Bal oldalra írod a mátrixot, jobb oldalra pedig az egységmátrixot. A cél ugyanaz: bal oldalon jöjjön ki az egységmátrix, ekkor jobb oldalon ott az inverz. Ha most az inverz tekintetében nézzük a lineáris egyenletrendszert (amit most Ax = b-nek írok), akkor az megoldható úgy (mindkét oldalt balról megszorozva A-1-el), hogy kiszámolod az x = A-1b szorzatot. A sok matekos handabandázás után itt az ideje, hogy konkrétan rákanyarodjunk a 3D grafika legfontosabb fogalmaira. A 3D világban kóválygó objektumok viselkedését úgynevezett affin leképezésekkel írjuk le, ami bár
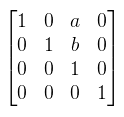
leírva bonyolultnak hangzik, valójában speciális mátrixokról van szó. Egy objektum minden eltárolt pontját beszorozva egy ilyen mátrixxal valósítható meg pl. az eltolás vagy forgatás.
Ez konyhanyelven azt jelenti, hogy ha két vektorra alkalmazok valamilyen transzformációt, majd az eredményvektorokat összeadom, akkor ugyanazt kapom, mintha előbb összeadtam volna őket és utána alkalmaztam volna a transzformációt. Ugyanez igaz skalárral való szorzásra is. Most tegyük fel, hogy V = W és vegyük az e1, ..., en bázist. Az előbbi definíció nyilvánvaló következménye (sőt, ekvivalens vele), hogy egy lineáris leképezés a lineáris kombinációt megtartja, azaz: 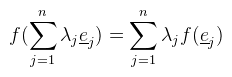 Na de: 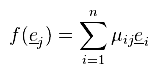 hiszen az ei-k, mint bázis minden vektort előállítanak, speciel az f(ej)-ket is. Mit látunk tehát ebből? Azt hogy minden lineáris transzformáció leírható egy hozzá (és az adott bázishoz) tartozó M := [ μij ] mátrixxal. Mondok is néhány példát lineáris transzformációkra (a konkrét mátrixokat egy külön bekezdésben sorolom fel): forgatás, nyújtás, tükrözés. Az eltolás nem lineáris transzformáció (hacsak nem toltad el...érted...hehehe...). Könnyű belátni, hogy miért nem: legyen f(x) := x + a, ekkor f(x) + f(y) = x + y + 2a és az nem egyenlő f(x + y)-al. Ennél tehát többet kéne megengednünk, hiszen jó lenne ha el tudnánk tolni pontokat. Affin transzformációnak nevezünk egy alakú leképezést, ahol M lineáris transzformáció. Itt már nem elég az, hogy V vektortér, hanem kell fölé egy úgynevezett affin tér (később). Van azonban egy rossz hír: ez nem írható le olyan mátrixxal, mint eddig, hanem be kell vezetni a fogalmát. Formális definíciót sajnos nem találtam, úgyhogy ebből és saját kútfőből voltam kénytelen dolgozni.
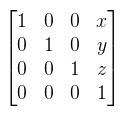
Előre is halmazt E3 projektív lezárásának hívjuk (de mivel úgyis pongyola vagyok, homogén térnek fogom hívni). Innentől fogva meg kell különböztetni a pont és a vektor fogalmát, tehát következzen az affin tér definíciója: Legyen V egy vektortér K felett, és vegyünk egy A nem üres halmazt. Definiáljuk az összeadást egy p ∈ A és egy a ∈ V között az alábbi módon:
Magyarázkodás nélkül egy p ∈ A elemnek feleltessük meg a (p1, p2, p3, 1)T homogén koordinátákat, amit ünnepélyesen elnevezek pontnak. Egy v ∈ V vektornak pedig feleltessük meg a (v1, v2, v3, 0)T homogén koordinátákat. A vektort is ünnepélyesen elnevezem vektornak, ezzel is diszkriminálva őt. Meglepő módon két pont különbsége egy vektor (a harmadik feltétel miatt). Nyilván a (wλ1, wλ2, wλ3, w) homogén koordinátából visszakapható az eredeti pont úgy, hogy végigosztasz w-vel. Ha ezt esetleg vektorra próbálnád megtenni, akkor egy értelmezhetetlen pontot kapsz, speciel az olyan irányú párhuzamos egyenesek metszéspontját. Ezzel a bővítéssel már mondhatjuk azt, hogy az affin transzformációkat 4x4-es mátrixxal írjuk le, mégpedig így: 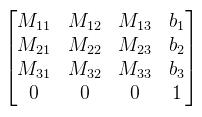 A pontok/vektorok pedig homogén koordinátákkal megadva ilyen mátrixxal szorozhatók. Speciel, ha M az egységmátrix, akkor az így kapott 4x4-es mátrix a b vektorral való eltolás mátrixa. Erről megint nem találtam formális definíciót, de talán nem is baj. Kétféle nevezetes vetítés van, amit tudni illik: perspektív és párhuzamos (szokták merőlegesnek is nevezni valami érthetetlen okból).
Itt most a perspektív vetítést vezetem le, mert az az érdekesebb.
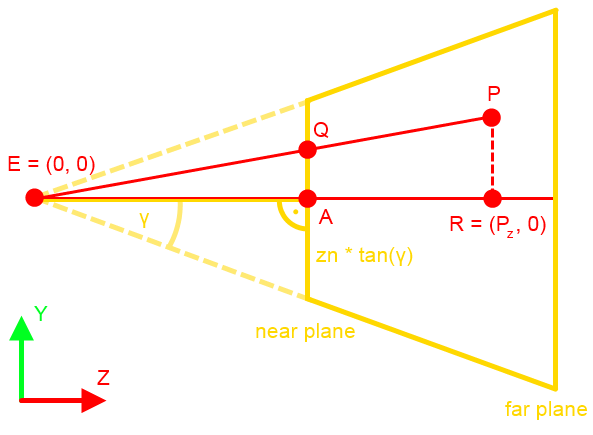 A frustum a következő paraméterekkel van megadva:
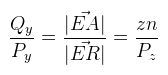 Ahonnan Qy kifejezhető. Van azonban még egy lépés, amit meg kell tenni: ezt a Qy-t le kell normalizálni a [-1, 1] intervallumba. Ez a következőképpen tehető meg: 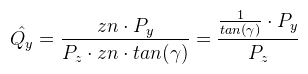 Ez nagyon jó, mert zn kiesett. Most nézzük meg ugyanezt az XZ síkban. Az ábrát teljesen ugyanígy kell elképzelni, csak fovy helyett egy fovx = 2δ szöggel. 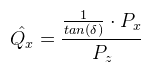 A kérdés az, hogy δ hogyan kapható meg γ-ból. Az is megoldható, de ennél van egy egyszerűbb képlet, hiszen ide tan(δ) kellene. Ezt megkapni baromi egyszerű, ugyanis: 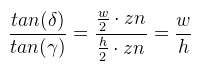 Ez azért tehető meg, mert a közeli vágósík (ha most, mint síklapot tekintjük) oldalai arányosak a képernyőhöz. Ez utóbbi w / h-t nevezzük el aspect-nek. Most nézzük hogyan építhető a két végeredményből mátrix. Rossz hír: sehogy, mégpedig a Pz-vel való osztás miatt. Ezért a 3D grafikában a vetítés két lépésre van osztva:
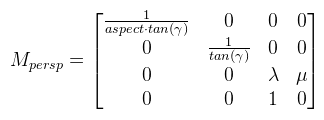 Ezzel beszorozva P-t kapod meg a (Qx, Qy, ?, Pz) clip space-beli homogén koordinátákat (device coordinates), melyet leosztva a w komponensével megkapod a képernyő koordinátákat a [-1, 1]2 tartományban (normalized device coordinates), de onnan konkrét pixelbe már könnyen átszámolható. Viszont van még pár kérdés, amit ?-el jelöltem, nevezetesen, hogy mi történjen z értékkel. A raszteres megjelenítésnek egy fontos tulajdonsága a z buffer, amit arra használ, hogy megmondja mely pixel van "legelöl". A z buffer tekinthető egy harmadik képernyőiránynak, legyen ez mélység (d). Ekkor a cél az, hogy Qz-t is kiszámoljuk, ugyanúgy a [-1, 1] intervallumba. Figyelembe kell venni, hogy a második lépésben leosztunk Pz-vel. Mit lehet tenni? A ?-ek helyett írjuk fel ami történni fog (vagy történhet): 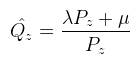 Hiszen Pw = 1. Végiggondolva adódik, hogy az xy koordinátákat fölösleges lenne belekeverni a buliba, ha μ = 0 lenne, akkor pedig az eredmény egy konstans, tehát λ is és μ is jogos és értelmes. Amit még tudunk az az, hogy ha Pz = zn, akkor az eredmény -1, illetve ha Pz = zf, akkor pedig 1. Ezt vadul írjuk is fel:  Amit vidáman meg tudunk oldani kézzel is, és az alábbi jön ki: 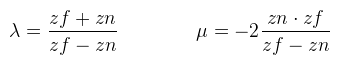 És ezzel kész a perspektív vetítési mátrix. Megjegyznék két fontos dolgot: én most itt úgy tekintettem, hogy a z tengely előrefelé mutat, de OpenGL-ben ez nem így van, tehát a mátrix megfelelő két elemét be kell szorozni -1-el. A másik dolog pedig, hogy DirectX-ben nem a [-1, 1] intervallumba kell kerülnie a Qz-nek, hanem a [0, 1]-be. Az így módosított mátrixokat az utolsó bekezdésben leírom. Ahhoz, hogy a vektoriális szorzatot definiáljuk, le kell rögzíteni a vektortér irányítását (handedness, nem lehet szebben lefordítani), ami pongyolán mondva a koordináta tengelyek irányát jelenti.
A jegyzet egy fantasztikus körmondatban definiálja ezt, amit nem fogok leírni, mert meg se próbáltam megérteni. Helyette mindenki előveszi a bal kezét, és a mutatóujját a monitor felé fordítva (z) a középső ujját jobbra (x), a hüvelykujját pedig felfelé (y) tartja.
Ez a balkezes koordinátarendszer (mily meglepő). Most mindenki előveszi a jobb kezét, a mutatóujj fölfele (y), a hüvelykujj jobbra (x), a középső ujj pedig magad felé (z) mutat. Ez a jobbkezes koordinátarenszer (mily meglepő). Mindkettő értelmes, ugyanis a fizkában
vannak olyan elektromágneses hullámok amelyek balkezes koordinátarendszert alkotnak (elektromos és mágneses mező iránya, illetve a haladási irány), de általában jobbkezest.
Ha most jobbkezes koordinátarendszert nézünk, akkor a mutatóujjad a, a középső ujjad b, és a hüvelykujjad a × b. Balkezes koordinátarendszerben a mutatóujj a × b, a középső ujj a, és a hüvelykujj b. Mindenekelőtt el kell mondani, hogy a vektorszorzás nem kommutatív. Másrészről csak 3 és 7 dimenzióban létezik, máshol nem (viszont más megközelítésekkel általánosítható). Harmadrészt pedig az eredményvektor merőleges az eredeti két vektorra. A középiskolás definíció a szorzat hosszára vonatkozik, azaz |a × b| = |a| |b| sin γ, amiből persze sin γ meghatározható, pláne ha a vektorok normalizáltak. Ha most veszünk n darab lineárisan független vektort, akkor azt mondjuk, hogy ezek ortogonálisak, ha bármely kettő skaláris szorzata 0 (azaz merőlegesek egymásra). Ha nem ilyenek lennének, akkor R3-ban a vektoriális szorzat segítségével ortogonalizálni lehet őket. Vegyünk 3 darab linárisan független vektort (a, b, c) amelyek nem ortogonálisak és legyen: b' := c' × a Ekkor az a, b', c' vektorok immár ortogonálisak. Magasabb dimenziókban ez értelemszerűen nem alkalmazható, helyette használható a Gram-Schmidt ortogonalizáció nevű módszer. Vegyünk most n darab linárisan független vektort (a1, ..., an) és legyen b1 = a1, ekkor az alábbi módon kiszámolt 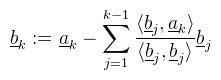 vektorok ortogonálisak. Ha még le is normalizálod ezeket, akkor azt mondjuk, hogy ortonormáltak. Ha egy olyan mátrixod van amelynek oszlopai orthogonálisak, akkor teljesül, hogy A-1 = AT. Azt, hogy egy mátrixnak létezik-e inverze többféleképpen is meg lehet mondani. Ehhez be kell vezetni néhány új fogalmat. Korábban említettem, hogy egy mátrix oszlopai tekinthetőek oszlopvektoroknak, hasonlóan a sorai pedig sorvektoroknak.
Az ezek által generált altereket oszlopvektor- illetve sorvektor térnek hívják. Mivel ezek alterek, van dimenziójuk, sőt az oszlopvektor tér dimenziója megegyezik a sorvektor tér dimenziójával (tetszőleges mátrixra).
Ezt a közös dimenziót hívják a mátrix rangjának.
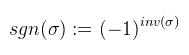 Ami tehát 1 ha σ páros, és -1 ha páratlan. Ekkor egy A ∈ Rnxn mátrix determinánsát a következőképpen lehet definiálni: 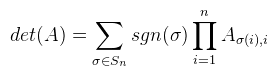 Ha most egy konkrét permutációt nézünk, akkor tehát a mátrix minden oszlopából kiválasztunk egy-egy elemet (a sor nem egyezhet meg), ezeket összeszorozzuk, és még megszorozzuk 1-el vagy -1-el a permutáció paritása szerint. Ha ezt minden permutációra megtettük, akkor az így kapott értékeket összeadjuk. A determinánst szokás így is jelölni: |A|. Mint mondtam, ezt a definíciót sosem használjuk, mert kezelhetetlen. Vannak azonban nagyon jó tételek, amikkel sokkal egyszerűbben is ki lehet számolni. Kezdjük rögtön azzal, hogy ha az A mátrix diagonális (a főátlóján kívül mindenhol 0), akkor a determinánsa a főátlóbeli elemek szorzata. Következésképp det(I) = 1. Ami nem látszik annyira, de fontos, hogy a mátrix determinánsa 0 akkor és csak akkor, ha a mátrix oszlopai (sorai) lineárisan összefüggőek. Ekkor inverze sincs. Most vegyünk egy A ∈ R2x2, tehát 2x2-es mátrixot, ekkor: 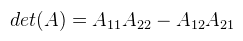 3x3-as mátrixra is adható viszonylag egyszerű képlet, csak épp a használt LaTeX szerkesztő nem bírta egy sorba bezsúfolni (egyébként is idegesít már), úgyhogy rögtön rátérek a Laplace-féle kifejtési tételre. Jelöljük aldet(A, i, j)-vel annak a részmátrixnak a determinánsát, amit úgy kapunk, hogy az i-edik sort és j-edik oszlopot kihúzzuk A-ban (így kapva egy kisebb mátrixot). Most rögzítsünk le egy i ∈ [1, n]-et, ekkor: 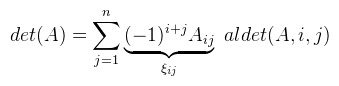 Tehát kiválasztod a mátrix valamelyik sorát (az i-ediket), és aszerint fejtesz ki, minden lépésben kihúzva a hozzá tartozó sort és oszlopot. A képletben ξij-vel jelölt elemekből a [ ξij ] kofaktor mátrix rakható össze. Megjegyezném, hogy ugyanígy oszlop szerint is ki lehet fejteni (sőt, tetszőleges permutáció szerint??). Példaként alkalmazzuk ezt egy 3x3-as mátrixra az első sor szerint kifejtve (és most |.|-el jelölöm az aldeterminánsokat, hogy kiférjen). 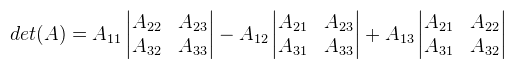 Ez a módszer kis mátrixokra elég gyors, nagy mátrixokra baromi lassú, de nekünk 4x4-esnél nagyobb úgyse kell. Nagyobb mátrixokra már érdemesebb az LU dekompozíciót használni (következő cikkben lesz róla szó). Még egy dolog van, ami itt fontos, ugyanis amennyiben a determináns nem nulla, a mátrix inverze kiszámolható az alábbi képlettel: 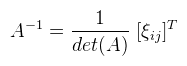 Ezt az utóbbi adj(A) = [ ξij ]T mátrixot az A mátrix adjungáltjának nevezzük. Ha A = adj(A), akkor a mátrix önadjungált. Egy korábbi cikkben már kifejtettem, hogy ez mire használható, de most leírom részletesebben. Vegyünk egy A ∈ Rnxn mátrixot, és a megfelelő I egységmátrixot.
Az A mátrix karakterisztikus polinomjának nevezzük az alábbi polinomot:
Emlékeztetőül polinom alatt egy véges összeget értünk, amely a0 + a1λ + a2λ2 + ... + anλn alakú. Például az x2 - 3 is egy polinom. A polinom foka a kifejezésben szereplő határozatlan (pongyolán: változó) legnagyobb hatványa (a példában tehát 2). A kA karakterisztikus polinom gyökeit (a.k.a. megoldásait) nevezzük az A mátrix sajátértékeinek. Az algebra alaptétele szerint egy n-edfokú polinomnak pontosan n darab gyöke van, megjegyzendő azonban, hogy ezek komplex számok is lehetnek, sőt a többszörös gyököket is beleszámoljuk. Azt mondjuk, hogy a v ∈ Rn vektor az A mátrix sajátvektora, ha teljesül valamilyen λ ∈ K-ra, hogy Av = λv. Vegyük észre, hogy: Ami egy lineáris egyenletrendszer. Ha most egy picit belegondolunk, hogy mikor lehet ez nulla, akkor rájöhetünk, hogy a skaláris szorzatnál megbeszélt azonosság miatt az A - λI mátrix minden sora merőleges v-re. Na de n dimenziós térben n + 1 vektor lineárisan összefüggő (a mátrix sorai és v), tehát a mátrix sorai nem lehetnek lineárisan függetlenek. Azaz a fenti egyenletnek akkor és csak akkor van megoldása, ha a lambdás mátrix determinánsa nulla. Tehát kilyukadtunk a karakterisztikus polinomnál, melynek megoldásai a most λ-val jelzett sajátértékek. A karakterisztikus polinom megkapható az említett Laplace-féle kifejtési tétellel (de mazochisták használhatják az eredeti definíciót). A gyökök kiszámolása után a sajátvektorok meghatározása már történhet ugyanúgy Gauss eliminációval. Természetesen, ha v egy sajátvektor, akkor a definíció szerint αv is az valamilyen α ∈ R-re. A sajátvektorok tehát egy alteret feszítenek ki, amit meglepő módon sajátaltérnek hívnak. A sajátértékeknek a halmazát pedig spektrum-nak szokták nevezni. Gyakorlati alkalmazás például az objektumhoz igazított befoglaló doboz kiszámolása. Szélsőséges esetben egy előre transzformált ponthalmazból is visszanyerhető egy (lineáris) transzformációs mátrix, de megjegyezném, hogy ez nem feltétlenül az, amivel eredetileg transzformálták (mint ahogy a befoglaló doboz sem az amit elvárnál). A duális tér fogalmát analízisben szokás inkább definiálni normált terekre, de én most azt nem fogom végigvezetni.
Ha most veszünk egy V vektorteret T felett, akkor egy φ : V → T lineáris leképezést szokás lineáris funkcionálnak is nevezni,
de ez a lineáris algebrában vizsgált esetekben kicsit pongyola feltételezés.
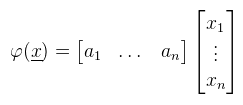 Innentől érthető, hogy miért kell megkülönböztetni a sor- és oszlopvektorokat, hiszen ha egy lineáris funkcionál megadható sorvektorral, akkor bódult állapotban mondhatunk olyanokat, hogy Rn duális tere önmaga. Józan állapotban viszont ez elég nagy ökörség, mint majd mindjárt látni is fogjuk. Egy kicsit visszakanyarodnék a bázistranszformációhoz, ahol is a célbázisbeli koordináták még mindig kiszámolásra várnak (de a megoldáshoz már fel vagyunk vértezve). Emlékeztetőül tehát a 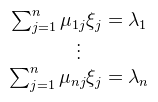 lineáris egyenletrendszert szeretnénk megoldani a ξ1, ..., ξn ismeretlenekre. Továbbra is jelöljük A = [ μij ]-vel az együtthatókból alkotott mátrixot. Legyen megint E = [ e1, ..., en ] a kiinduló bázis és F = [ f1, ..., fn ] a célbázis, és mint ahogy megbeszéltük F = EA teljesül (mint mátrixszorzás). Írjunk most fel egy tetszőleges x ∈ V vektort a kiinduló bázisban: 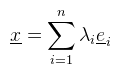 És jelöljük xe = (λ1, ..., λn)T-vel az x vektor kiinduló bázisra vonatkozó koordináta oszlopát. Ekkor az előbbi lineáris kombináció felírható mátrix-vektor szorzásként: 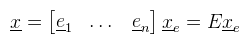 De mivel fi is bázis, az is hasonlóan előállítja x-et, tehát: 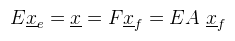 És az egyenlet mindkét oldalát balról beszorozva E-1-el, majd A-1-el kapjuk, hogy: 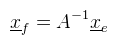 És megkaptuk a keresett xf = (ξ1, ..., ξn)T koordináta oszlopot a célbázisban. A koordináta oszlopok tehát a bázisváltás mátrixának inverzével transzformálódnak. Ezen fellelkesedve azt mondjuk, hogy az x ∈ V vektorok kontravariánsak. Most vegyünk egy φ = (a1, ..., an) lineáris funkcionált V*-ból és vezessük be az alábbi jelölést: 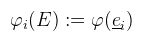 Ami tehát a funkcionál alkalmazva az i-edik kiinduló bázisvektorra (és továbbra is skalár). Következő lépésként kezdjük el számolni ugyanezt a célbázisban: 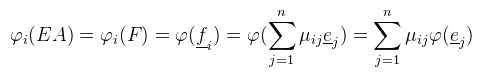 Az átalakítás megtehető, mert φ lineáris. Az eredmény még mindig n darab skalár, amit írjunk fel egy sorvektorba és jelöljük φ(E) = (φ1(E), ..., φn(E))-vel. Ekkor úgy mint előbb, az egyenlőség felírható mátrix-vektor szorzásként, azaz: 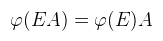 A lineáris funkcionál tehát ugyanúgy az A mátrixxal transzformálódik, mint a bázis. Ezt pedig úgy mondjuk, hogy a φ ∈ V* egy kovariáns vektor. Aki 3D grafikázott már annak furcsák lehetnek az itt leírtak, mert látszólag pont fordítva van, mint ahogy azt alkalmazni szoktuk.
Úgyhogy akkor most kifejteném, hogy miről volt szó eddig és a 3D grafikában miért van (látszólag) máshogy.
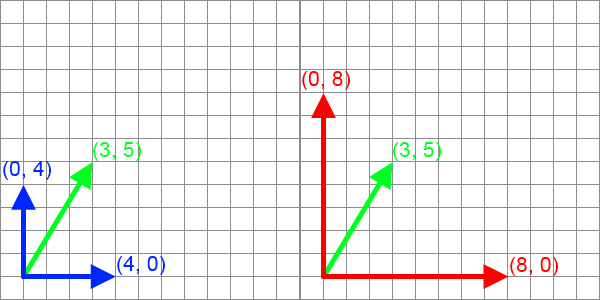 Amiről a cikk elején beszéltünk az volt, hogy ugyanazt a vektort írjuk fel a másik bázisban. Könnyű kiszámolni, hogy a kék bázisban a koordináta oszlop (3/4, 5/4)T a piros bázisban pedig (3/8, 5/8)T, azaz valóban a bázisvektorok transzformációjának inverzével szorzódik (tehát mivel kétszeres nyújtást nézünk, feleződik). Általában viszont nem ugyanazt a vektort akarod, hanem a lineáris kombinációt megtartva keresed az új vektort, azaz egy lineáris transzformációt alkalmazol: 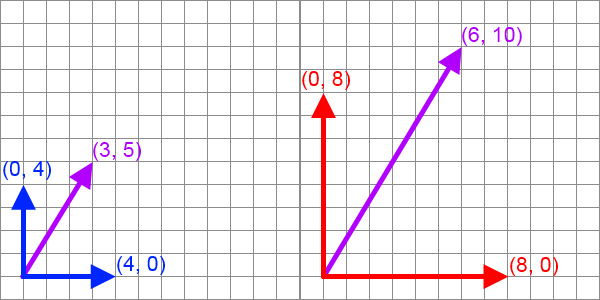 Ez tehát egy alapvető különbség a bázistranszformáció és a lineáris transzformáció között. A kavarodást az okozza, hogy Rn-ben a koordináta oszlopok is és a duális tér elemei is ugyanolyan vektornak tekinthetők, sőt affin térként tekintve rá még a pontok is ugyanúgy írhatóak le. Rn tehát ilyen "sokféleképpen értelmezhető" tér (de azért ne legyen félreértés: rengeteg olyan fontos tér van, ami nem ilyen!). Most tekintsük úgy, hogy Rn affin tér és vegyünk egy p pontot. Rögzítsük le az origót a (0, 0, 0) pontba, ekkor p-t tekinthetjük helyvektornak, tehát használható rá a mátrixxal való szorzás. Mostantól fogva az objektumod minden pontja ilyen pont. Pont ilyen. Egy lineáris transzformációt (M) alkalmazva rá p' = Mp az új pont. Ez a lila nyíl, és kontravariáns vektor. Pont. Most vegyünk egy funkcionált, mondjuk a példa kedvéért egy síkegyenletet, ami a klasszikus egyenlettel írható le. Ami nem lineáris funkcionál, csak hogy könnyű legyen a dolog. Affin funkcionál nincs. Segítségül hívva a homogén koordinátákat viszont leírható így: Ebbe az egyenletbe írjuk be középre az egységmátrixot, mégpedig így: De persze a mátrixsszorzás asszociatív, tehát azt lehet mondani, hogy a síkegyenletet, mint kovariáns vektort a lineáris trafó inverz transzponáltjával kell szorozni. Ez nem a zöld nyíl, de hasonlóan képzelhető el és például az objektum normálvektorait így kell trafózni. A bázistranszformáció nem keverendő össze a lineáris transzformációval. Az alábbi táblázatban mégegyszer összefoglalom a lényeget:
A bázistrafó tehát koordináta oszlopokra, illetve funkcionál értékekre vonatkozik, az affin trafó viszont pontokra/vektorokra illetve magára a funkcionálra. A táblázatból a második oszlopot kell megjegyezni, ugyanis az affin és projektív trafók használatosak mindenre 3D grafikában. A cikk végén következzenek a leggyakrabban használt (lineáris és projektív) transzformációk mátrixai, ahol nem írom ki külön ott balkezes koordinátarendszerben. Egyrészt azért mert a DirectX-es cikkekben azt használok, másrészt mert sokkal természetesebb mint az elcseszett OpenGL-féle jobbkezes maszturbálás (de valójában csak a vetítések és némelyik forgatás különböző).
Ugye mindenki látja a transzponálás jelét a DirectX-es mátrixban? És ugye mindenki látja, hogy az y tengelyen való forgatásnál máshol van a negatív szinusz? Részletesebben lásd a megfelelő DirectX és OpenGL függvények dokumentációját.
Summarum
Régen volt ennyi kép egy cikkben.
A gyakorlatban sokkal könnyebb alkalmazni az itt leírtakat, amíg a "klasszikus" 3D grafikánál maradsz. A haladóbb algoritmusok megértésehez viszont még ennél is mélyebbre kell menni, például a mátrixok még tovább általánosíthatóak
tenzorokká, a mátrixsszorzás pedig kontrakcióvá. És igen, azt is kellett már alkalmaznom.
|