|
Az előző fejezetben volt ilyen, hogy normal mapping, sőt meg is jegyeztem, hogy a csalás ellenére tisztán látszik, hogy a felület lapos. Nézzük meg miért van ez:
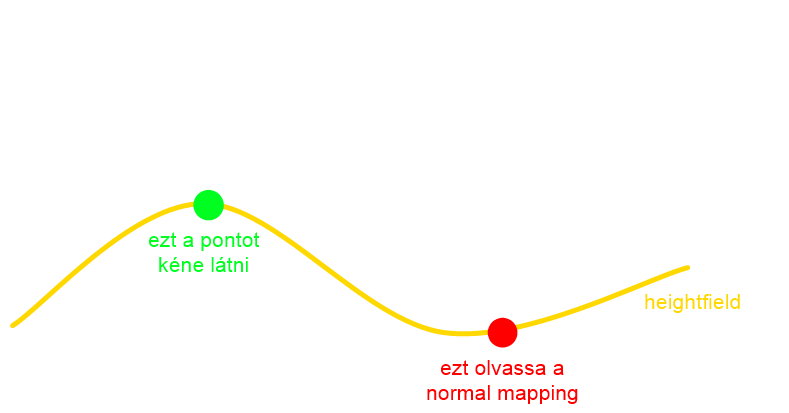
Tehát a normal mapping a felület alakjából semmilyen információt nem vesz figyelembe, csak a normálvektort használja fel a megvilágításhoz. Ez egyszerűbb felületeknél (pl. téglafal) elegendő lehet, sőt még gyors is, de általában sokkal realisztikusabb hatást akarsz elérni.
Para-e a parallax?
Először is mi az hogy parallax: ha úgy tetszik egy optikai csalódás: egy közeli objektumnak a pozíciója (pl. mi előtt van) látszólag megváltozik ha két különböző helyről nézed. Mondjuk amikor mész az autóval és kinézel balra, akkor
a melletted sétáló öreg néni természetét meghazudtoló sebességgel zúz el, míg a távolban a fák mozdulatlanok.
CODE
float heightBias = 0.01f;
float heightScale = 0.2f;
float3x3 tbn = { wtan, -wbin, wnorm };
// nézési irány
float3 p = vdir;
float3 v = normalize(vdir);
float3 s = normalize(mul(tbn, v));
// az aktuális magasságból kiszámolunk egy offsetet
float curr = tex2D(mytex1, tex).a;
float height = (1 - curr - heightBias) * heightScale;
float x = length(s.xy);
float off = (x * height) / s.z;
// a "-" csak a szokásos korrekció a tbn-hez
float2 dir = normalize(float2(-s.x, s.y)) * off;
tex += dir;
p.xy += dir;
// TODO: megvilágitás, stb.
Ez a shader egyszerű és olcsó, viszont erősen korlátozott. Minél jobban növelem a buckásodást, annál jobban szétcsúszik az egész, mintha legalábbis a radiátor gombjait tekergetném. Sőt, a domború hatást is csak addig éri el, amig közel merőleges szögből nézel rá, ami lássuk be, hogy alig jobb mint a normal mapping. Az alábbi ábra szemléteti, hogy mit is csinál: 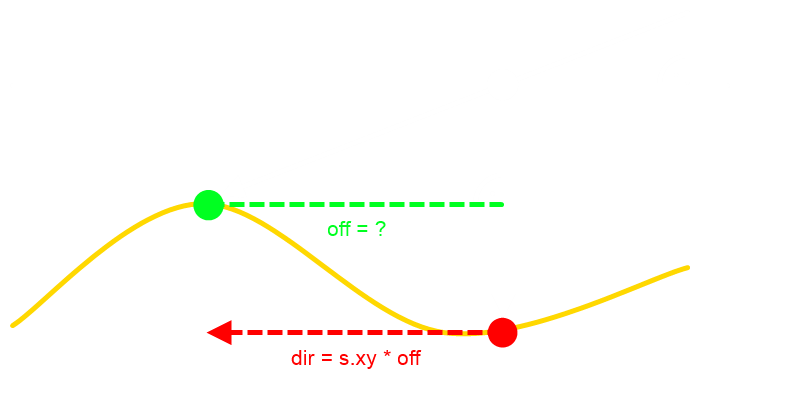
Ez egy saját értelmezésem a módszerről (de a DirectX SDK-ban is ilyesmi van). Ha megnézzük a két háromszöget, akkor feltűnhet, hogy hasonlóak, tehát a megfelelő oldalak aránya megegyezik. A probléma, hogy a bias-t nem ismerjük és emiatt hal meg a módszer. Maximum feltételezést lehet tenni, ami téglafalnál még viszonylag egyszerű, de ott is csak addig amíg nem tolod ki nagyon a téglákat. Megjegyezném, hogy az eredeti paperben (kézzel kell lementeni) levő megoldás látszólag mást csinál, de ott is ugyanaz a probléma: a keresett pontbeli magasság kellene neki, de azt nem tudja, ezért approximálja az aktuális helyen levővel. Ez világos, hogy egy nagyon durva becslés és gyakorlatilag sosem igaz. Annyit hozzáfűznék, hogy a view vektort le kell vetíteni az tn illetve bn síkokba, és akkor lehet kiszámolni az említett szögeket. Ez kódban valami ilyesmi, de nem tudom megerősíteni a helyességét, mert az eredmény katasztrofális. CODE
float3 t = normalize(wtan);
float3 b = normalize(wbin);
float3 n = normalize(wnorm);
float2 newtex;
float depth = tex2D(mytex1, tex).a;
float tan1, tan2;
float3 eu = normalize(vdir - dot(vdir, b) * b);
float3 ev = normalize(vdir - dot(vdir, t) * t);
// kihasználva, hogy tan(a) = sin(a) / cos(a)
tan1 = length(cross(eu, n)) / -dot(eu, n);
tan2 = length(cross(ev, n)) / -dot(ev, n);
// ez az ami nem igaz: ugyanis depth = tex2D(mytex1, newtex).a kellene
newtex.x = tex.x + tan1 * depth;
newtex.y = tex.y + tan2 * depth;
Höfö egyrészt találni egy olyan textúrát amire jó, másrészt megjavítani, ha esetleg elrontottam volna.
Parátlan és páratlan okklúzsün
Rövid idő alatt sokan rájöttek, hogy nem lehet megúszni a dolgot valamiféle iteratív keresés nélkül, sőt olyan jól sikerült ez nekik, hogy ugyanazt a módszert elnevezték
ötvenféleképpen. Néhány elnevezés ezek közül: steep parallax mapping,
parallax occlusion mapping,
relief mapping.
Gyakorlatilag ugyanazok (heightfield tracing), legfeljebb abban van különbség, hogy milyen módszert használnak a metszetkereséshez.
Egy fontos aspektusa ezeknek a cuccoknak, hogy self shadowing-ot is el lehet érni velük. Azaz a felület most már nem csak buckás, hanem árnyékos is lehet.
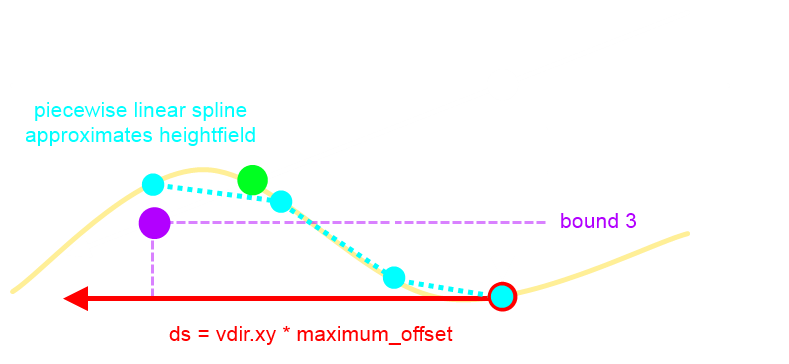
Az ábra az iteráció néhány lépését mutatja. A ds vektor mentén lépkedünk, és azt vizsgáljuk, hogy a felület alatt vagyunk már-e. Ha még nem (bound 1-2), akkor lépünk tovább a vektoron és az z tengelyen, de eltároljuk az előző állapotot is. Előbb-utóbb elérünk egy olyan ponthoz ami a felület alatt van már (lila pötty, illetve bound3), ekkor behatároltuk a keresendő pontot és az eltárolt információ alapján (két világoskék, a lila és egy nem felrajzolt fehér pötty) meghatározható a metszet. Világos, hogy ez nem feltétlenül esik egybe a zöld pöttyel (az ábrán sem), de nem fog artifactokat okozni. CODE
// dp = ez a rendes texkoord
// ds = view vektor levetítve a tb síkba; a hossza a lehető legnagyobb offset (háromszögek hasonlóságából)
float2 computeParallaxOffset(float2 dp, float2 ds, int numsteps)
{
int i = 0;
float stepsize = 1.0 / (float)numsteps;
float curr = 0.0; // vizsgálandó magasság
float prev = 1.0; // előző magasság
float bound = 1.0; // 1-től indul, hiszen ez a lehető legnagyobb
float2 offstep = stepsize * ds; // ennyit lépünk egy iterációban a ds mentén
float2 offset = dp; // itt vagyunk éppen a texkoorddal
float2 pt1 = 0;
float2 pt2 = 0;
while( i < numsteps )
{
// lépünk a textúrában
offset += offstep;
curr = tex2D(mytex1, offset).a;
// és y-on is
bound -= stepsize;
// ha átlépték egymást
if( curr > bound )
{
pt1 = float2(bound, curr);
pt2 = float2(bound + stepsize, prev);
// kész, kiléphetünk
i = numsteps + 1;
}
else
{
i++;
prev = curr;
}
}
// tegye fel a kezét, aki érti (de nem nehéz levezetni)
float d2 = pt2.x - pt2.y;
float d1 = pt1.x - pt1.y;
float d = d2 - d1;
float amount = 0;
if( d != 0 )
amount = (pt1.x * d2 - pt2.x * d1) / d;
return dp + ds * (1.0f - amount);
}
Ehhez már érdemes SM 3.0-t használni, de meg lehet oldani SM 2.0-val is (csak nem sok értelme van). Itt dp a kiinduló pont (tex), ds pedig a maximális offset ami csak szóba jöhet. A fenti háromszöges meggondolással ezt egyszerűen ki lehet számolni, például ebből pedig maxoff = vdir.xy * tg α. Fontos, hogy vdir itt normalizálatlan. Világos, hogy a pontatlanság az iterációk számával javítható. Viszont csak akkor van szükség sok iterációra (azaz kis lépésközre a ds-en), amikor nagyon éles szögből nézed a felületet. Legyen ez a lépésköz a nézési irány felülettel való bezárt szögének függvénye (ami barátok közt is kiszámolható dot-al), konkrétan a kapott [0, 1]-beli értékkel lerp a minimális és maximális iterációszám között. Nyilvánvaló, hogy ha ez elég nagy, akkor azt a sebesség bánja.
A rilíf az rilétid?
Miért jók a bináris keresőfák? Például azért mert a fa magasságával arányos lépésszámban megtalálják a keresett pontot. Csináljuk a következőt: felezzük meg a ds vektort
és nézzük meg, hogy a közepén a felület alatt vagy felett vagyunk-e. Ha alatta vagyunk, akkor csináljuk ugyanezt a jobb oldali részre, ha felette akkor a bal oldalira.
Világos, hogy viszonylag gyorsan megtalálja a pontot, csak éppen elvi hibás (bár höfö volt, elmondom: azért mert a felezési pont lehet, hogy a felület alatt van, de a keresett pontot még ez előtt kellene megtalálni,
amit átugrottál; azaz folytatni kellene a keresést jobbra, csak erről nem tudsz).
CODE
float rayIntersectHeightfield(float2 dp, float2 ds)
{
const int linear_search_steps = 15;
const int binary_search_steps = 15;
float4 t;
float size = 1.0f / linear_search_steps;
float depth = 0.0f; // hol tartunk éppen
float best_depth = 1.0f; // az eddigi legjobb mélység
// megkeressük az első olyan pontot, ami már a felületen belül van
for( int i = 0; i < linear_search_steps - 1; ++i )
{
depth += size;
t = tex2D(mytex1, dp + ds * depth);
if( best_depth > 0.996f )
{
if( depth >= (1.0f - t.w) )
best_depth = depth;
}
}
depth = best_depth;
// a talált pont környezetében keressük a pontos metszést
for( int i = 0; i < binary_search_steps; ++i )
{
size *= 0.5;
t = tex2D(mytex1, dp + ds * depth);
if( depth >= (1.0f - t.w) )
{
best_depth = depth;
depth -= 2 * size;
}
depth += size;
}
return best_depth;
}
Érdekes ötlet, de lassabbnak tűnik mint az előző. A heightfieldtől függ...lehet hogy az első pontot könnyű megtalálni, amihez kevés lineáris lépés kell és akkor a bináris keresésnek van hozadéka. De ennek nyilván a fordítottja is lehet: sok lineáris, és akkor ugyanott tartasz, mint a parallax occlusionnal. Átlagos esetben viszont mindenképpen ez a gyorsabb.
Self shadowing
A legegyszerűbb megoldás az, hogy a fenti rayIntersectHeightfield függvényt meghívod mégegyszer, a fény irányvektorára. Ezzel viszont az ányékok pixelesek és kontrasztosak (hard shadows).
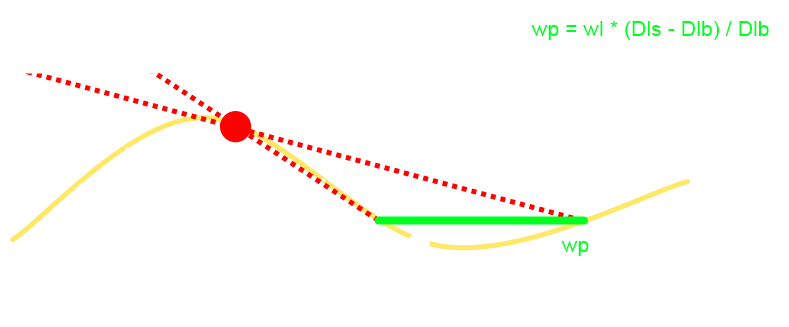
Egyszerűen látszik, hogy a felület magassága az adott pontban h = Dls - Dlb, ez az amit ismerünk (heightmap). Amit nem tudunk az az, hogy melyik a heightfield (lokálisan) legmagasabb pontja, hiszen az fog árnyékot vetni. Azt mondja erre az ATI, hogy a (tb síkba levetített) fényvektor mentén vegyünk mintákat, válasszuk ki a legnagyobbat és számoljunk azzal (és abból jön ki Dlb, azaz a fény-árnyékvető távolság): CODE
float sh0 = tex2D(mytex1, tex).a; // Dls
float softy = 0.58f; // wl, ezt te döntöd el mekkora
// shi = (Dlb - Dls - tökömtudja) * (1 / Dlb_kene_legyen) * wl
float shA = (tex2D(mytex1, tex + l.xy * 0.88f).a - sh0 - 0.88f) * 1 * softy;
float sh9 = (tex2D(mytex1, tex + l.xy * 0.77f).a - sh0 - 0.77f) * 2 * softy;
float sh8 = (tex2D(mytex1, tex + l.xy * 0.66f).a - sh0 - 0.66f) * 4 * softy;
float sh7 = (tex2D(mytex1, tex + l.xy * 0.55f).a - sh0 - 0.55f) * 6 * softy;
float sh6 = (tex2D(mytex1, tex + l.xy * 0.44f).a - sh0 - 0.44f) * 8 * softy;
float sh5 = (tex2D(mytex1, tex + l.xy * 0.33f).a - sh0 - 0.33f) * 10 * softy;
float sh4 = (tex2D(mytex1, tex + l.xy * 0.22f).a - sh0 - 0.22f) * 12 * softy;
float shadow = 1 - max(max(max(max(max(max(shA, sh9), sh8), sh7), sh6), sh5), sh4);
shadow = shadow * 0.3 + 0.7;
diffuse *= shadow;
specular *= shadow;
Ha valaki érti, hogy miért kell levonni az offsetet, az elmondhatná. Nekem gözöm nincs, ezért az implementációmban nem is vonom le. Az utána levő szorzás szintén csalás szagú, valószínüleg 1 / Dlb-t akarja közeliteni, de valami teljesen unortodox módon. Az ATI ezt nem részletezi, úgyhogy ennyit tudtam tenni. Az árnyék mindenesetre puha és még majdnem látszik is. Döntse el mindenki, hogy kell-e.
Summarum
Melyik a legjobb? Ezt nem lehet így eldönteni, mivel mindegyik módszer folyamatosan fejlődik (pl. interval mapping), sőt van hogy új módszerekre is ráfogják, hogy az például relief mapping. Nyilvánvalóan a hardver határozza meg, hogy
melyiket használhatjuk, így mindenképpen érdemes visszaskálázhatóvá tenni.

Bal oldal: normal mapping, jobb oldal: relief mapping. Totál azt hinnéd, hogy valódi geometria :) A fejezetben megmutattam hogyan lehet a normal mappingot feljavítani úgy, hogy ténylegesen domború felületeket kapjunk. A módszerek további előnye, hogy önárnyékolást is képesek kezelni, illetve ha az eltolt pontok mélységét is újraszámolod, akkor a jelenetbe is megfelelően illeszkedik (depth test!). Egy lényegesebb továbbfejlesztése a módszernek az ami már az objektum sziluettjére is képes buckákat tenni (pl. egy téglafal szélei pont szemből nézve). Erről lehet olvasni az ATI paperében. Tegye fel a kezét, aki érti (nem magyarázzák túl, egy oldal az egész...). A cikk kódja letölthető itt. Höfö:
|
