|
A 3D megjelenítés örök vesszőparipája az úgynevezett "fotorealizmus", amit azért tettem idézőjelbe mert szubjektíven ítélik meg: 2004-ben a Half-Life 2 volt fotorealisztikus, 2007-ben meg a Crysis. Mostanra már egyiket sem mondanánk annak.
A physically based rendering (PBR) szakít ezzel a szubjektivitással és egy objektívabb, fizikai modellre alapozva minősíti az előállított képet.
TartalomjegyzékNa de mit is jelent ez a PBR? Egyáltalán hogyan kell lefordítani magyarra? Én úgy fordítom magamnak, hogy (fény)fizikán alapuló megjelenítés, mert ez rögtön meg is magyarázza a jelentését. Eddig a megjelenítő enginek ad-hoc jellegűek voltak, tehát egy jelenet adott (fény)beállításokkal tök szép volt, más környezetben viszont a hackelések miatt tipikusan rosszul nézett ki (nappal vs. este, belső tér vs. külső tér). A PBR legfontosabb jellemzője tehát, hogy vizuális minőség helyett mérhető fizikai mennyiségek alapján validálja az előállított képet. Összefoglalva:
Ez az alap anyagmodell, és az egyszerűségéhez képest meglepően sokféle anyag közelíhető vele. Persze a mainstream enginek ennél többet is megengednek; pl. az UE4 blueprintjeivel tetszőlegesen komplex anyagokat lehet létrehozni, de ezekkel nem foglalkozom. Szintén nem foglalkozom átlátszó anyagok megjelenítésével, hiszen már írtam róla cikket, amiből kiderül, hogy fizikailag korrekten igen nehézkes ezeket megjeleníteni. Ha a korrektségtől (fénytörés) eltekintünk, akkor üvegszerű dolgokat össze lehet buherálni premultiplied alpha blending-el. A 2015-ös SIGGRAPH-on azóta megjelent a Disney új jegyzete, ami kiterjeszti a módszert átlátszó anyagokra is. Designereknek ajánlott elolvasni ezt meg ezt (regisztrálni kell). Először is egy kis emlékeztető differenciál- és integrálszámításból. Az f: R → R függvény differenciáljának nevezzük a
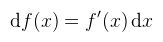
függvényt. A differenciál konyhanyelven "f(x) megváltozása, amikor x megváltozása dx". Azért foglalkozunk ezzel, mert magasabb dimenziókban könnyebben lehet vele számolni, mint a deriválttal (amit esetleg nem is ismerünk). A differenciálás inverz művelete az integrálás: 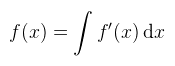
amin senki nem lepődik meg. Az [a, b] intervallumon vett Riemann integrálra gondolhatunk úgy, hogy az intervallumot felosztjuk végtelenül kicsi dx részekre, ezeken kiértékeljük az integrandust, majd az eredményeket összeadjuk. Ahogy dx tart 0-hoz, úgy az összeg is tart az integrálhoz. A továbbiakban elszakadok a Riemann integráltól és egy általánosabb fogalommal, a felületi integrállal fogok dolgozni. A következő fontos fogalom a térszög, ami a konyhanyelven értett 2D-s szög kiterjesztése 3D-be. Először gondoljuk végig, hogy a konyhanyelven értett szög mit jelent: egy α szög radiánban kifejezve megfelel a szög által az egységkörből kimetszett körív hosszával. Két szög különbsége egy dα differenciális szög. Ha analóg módon gondolkozunk, akkor 3D-ben egy Ω térszög megfelel az egységgömb felületén általa kimetszett területtel, szteradiánban (sr). Ahogy 2D-ben a szög, úgy 3D-ben a térszög is meghatároz egy irányvektort, amit két rendes szöggel lehet megadni (φ ∈ [0, 2π] és θ ∈ [0, π]). Kicsit zavaró, hogy az irodalmak ezt az irányt szokták (aláhúzás nélkül) 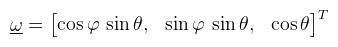
-val jelölni és az ebben az irányban értelmezett (differenciális) térszöget dω-val. A differenciális térszöget úgy kell érteni, hogy "φ és θ megváltozása által meghatározott térszög". Mivel ω egyben paraméterezése is az egységgömbnek: 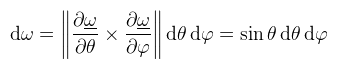
Vajon mi történik, ha integráljuk? 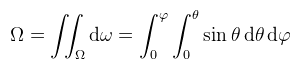
(megjegyzés: integráljelből ahol lehet, ott mostantól csak egyet fogok kiírni) Bal oldalon az Ω térszögön vett felületi integrál van, azaz az Ω térszöget felosztjuk végtelenül kicsi dω differenciális térszögekre, majd ezeket összeadjuk és (mily meglepő) visszakapjuk Ω-t. Jobb oldalon ugyanez egy dupla Riemann integrálként kifejezve. Ha Ω a teljes gömbnek megfelelő térszög (S), akkor φ = 2π és θ = π, így az eredmény 4π szteradián. Ha Ω csak a félgömbnek megfelelő térszög (H), akkor az eredmény 2π szteradián. Az integráljel alatt a továbbiakban az Ω jelölést fogom használni, de tipikusan félgömböt fogok érteni alatta. Ha esetleg más térszögön integrálok, azt külön jelzem. Ez eddig könnyű volt, de most jön valami nehezebb: egy tetszőleges felület által kifeszített térszög, ami a felületnek az egységgömbre való vetületének a területe (tehát ezt már nem mindig lehet Riemann integrálként felírni). Ha most veszünk egy végtelenül kicsi dA felületdarabkát, akkor az általa kifeszített dω (differenciális) térszög kiszámítható az ábrán látható módon: 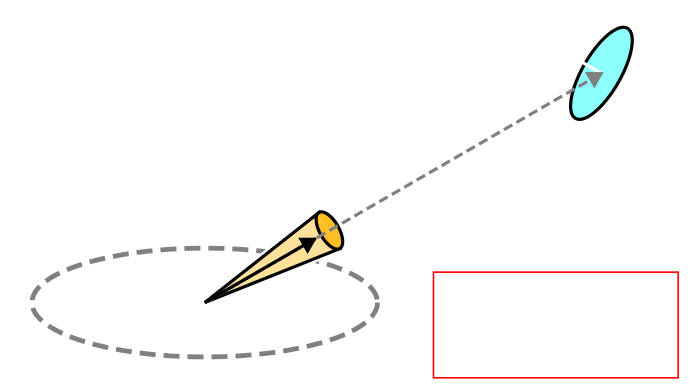
Ugye mindenki látja, hogy ez itt θ'? Az irodalmak ilyen szempontból elég szórakozottak, hogy nem képesek valami más szimbólumot találni. Egy konkrét felület által kifeszített térszög az ilyen felületdarabkákon vett felületi integrál. Ezzel most nem foglalkozok tovább, de a képlet fontos lesz később. (megjegyzés: ω alatt innentől én is ω-t értem, dω alatt pedig egy végtelenül kicsi térszöget körülötte) A fény egy elektromágneses hullám, azaz van elektromos és mágneses mezője, sőt ezek a haladási irányra merőlegesen oszcillálnak (transzverzális hullám).
Két hullámhegy távolsága a hullámhossz, ezt λ-val jelölik. A számunkra látható fény hullámhossza 380 és 780 nanométer között lehet. Az anyag fényre gyakorolt hatását az anyag törésmutatója mondja meg, ez változhat attól függően, hogy milyen hullámhosszú fénnyel találkozik.
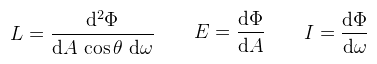
(megjegyzés: mivel a radiancia egy adott irány mentén halad egy adott pontból vagy pont felé, ezért L(x, ω)-nak kéne írni, de a paramétereket lustaságból el szokták hagyni) Ahol θ a pontbeli normálvektor és ω által bezárt szög. Most rögzítsünk le egy ωi bejövő irányt, a körülötte levő dωi térszöggel. Az ebből az irányból beérkező radianciát jelölje Li(ωi), ekkor az első képletet átrendezve: 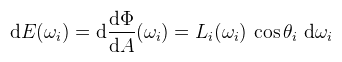
Ha esetleg integráljuk a pont körüli félgömbön, akkor megkapjuk az irradianciát (ez később fontos lesz). Most viszont a kimenő iránybeli radianciát szeretnénk tudni, tehát Lo(ωo)-t. Most jön egy meglepő feltevés: dLo(ωo) arányos dE(ωi)-hez, és ezt az arányt nevezzük BRDF-nek (bidirectional reflectance distribution function), ami tehát: 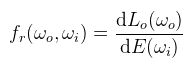
Ez egy definíció; akinek megvan az eredeti dolgozat az utánaolvashat, hogy miért ilyen. Mindenesetre behelyettesítve az előbbit, illetve kifejezve dLo(ωo)-t: 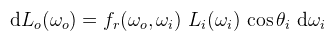
És mondjuk integráljuk a pont körüli félgömbnek megfelelő térszögön: 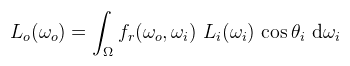
Ez az úgynevezett tükröződési egyenlet (reflectance equation, de máshol radiance equation-nak is mondják). Itt a könyv jelöléseivel voltam konzisztens, de egy kicsit kibogozva a szálakat: ωi az eddig megszokott fényirány (l), ωo a nézési irány (v), cos θi pedig a szokásos n·l. Nem kell megrettenni az integráltól sem: analitikus fényforrások (pl. pont fény) esetén meglepő módon van analitikus megoldása, szélsőséges esetekben pedig Monte Carlo integrálással közelíthető. Először is a legszimpatikusabb tulajdonsága, hogy mérhető. Az interneten található MERL adatbázis 100 féle anyag BRDF-jét tárolja, 3D tömb formában. A Disney készített egy programot, ami meg tudja jeleníteni ezeket, de a PBR-hez szükséges paramétereket próba-szerencse alapon kell kikövetkeztetni...
Ez alapján most mutatnám be a Lambert-féle diffúz BRDF-et, ami rettentően bonyolult: 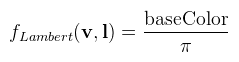
A π-vel való osztás az energiamegmaradás miatt kell, ugyanis a cos integrálja a félgömbön pont π. Mily meglepő, hogy az eddigi cikkeimben én sem, de mások sem vették ezt figyelembe. Máris egy kicsit fizikaibbnak érezhetjük ettől magunkat, csak az a szépséghiba, hogy Lambert felületek nincsenek a valóságban (viszont a matt felületeket jól modellezi). Az eddig megszokott módon a BRDF-et most is két részre osztjuk: egy diffúz (fd) és egy spekuláris (fs) komponensre. Előbbinek a Lambert teljesen jó, bár a Disney és a DICE ezzel nem ért egyet (a Disney-féle diffúz BRDF figyelembe veszi a durvaságot is). A Crytek szintén nem, ők az Oren-Nayar modellt használják. Az igazi buli a spekuláris komponenssel van, ugyanis arra a Cook-Torrance-féle általánosított mikrofelület modellt fogom használni (mint ahogy majdnem mindenki más is). Ez egy több tagból álló függvény, így a végeredménynek több variációja is lehet, az egyes részegységek megválasztásától függően. De előbb egy rajz: mit jelent a felület durvasága? (tipp: nem azt, hogy beszól neked a villamoson): 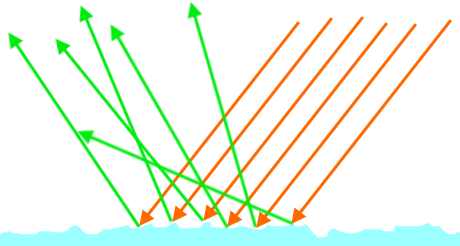
Ahogy mondtam, "rücskös", tehát a beérkező fénysugár mindenféle véletlenszerű irányban törik meg a mikrofelületek miatt, ettől a tükröződés mosottas lesz. Természetesen ezeket a mikrofelületeket nem szimuláljuk explicit, csak egy eloszlásfüggvényt adunk meg a félvektor (h = normalize(l + v)) alapján. 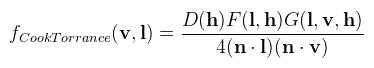
A részegységek magyarázata:
A három közül a legegyszerűbb F, mert erre szinte mindenki a Schlick-féle közelítést használja (az UE4 kicsit módosít rajta): 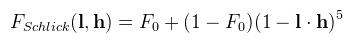
Ahol F0 a Fresnel-egyenlet értéke 0 fokos beesési szögnél: szigetelő anyagokra konzisztenesen 0.04 (mert amúgyis ekörül mozog), fémekre pedig a fém színe (pl. arany esetén (1.022, 0.782, 0.344)). Az irodalmak közötti eltérés leginkább D és G megválasztása. A már említett BRDF Explorer-ben sokfélét ki lehet próbálni, de én lusta módon azokat választottam, amiket az irodalmak propagálnak, tehát D-nek a GGX függvényt: 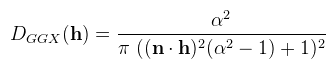
Ahol α = rougness2 (a Disney javaslata alapján). Hátravan még G, erre az UE4 által preferált Smith-Schlick közelítést használtam: 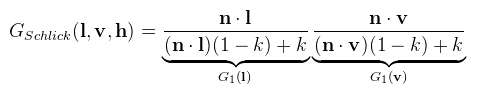
Ahol k = (roughness + 1)2 / 8 analitikus fényekre (szintén Disney javaslata), de k = roughness2 / 2 light probe-okra. Kipróbáltam még a DICE-féle Smith-GGX megoldást is, de végül nem használtam (nem azért mert ronda, hanem CSAK). Ha ránézünk erre a függvényre, akkor majdnem kiejti a Cook-Torrance nevezőjét, ezért optimalizációs célból egy Vis nevű függvénynek szokták definiálni, amiben ez az egyszerűsítés már benne van. Ezekkel a függvényekkel igazából nem szükséges ennél részletesebben foglalkozni, hacsak nem utánaszámolás céljából. Amit még tisztába kell tenni az a fénykezelés, illetve hogy milyen fényekkel foglalkozik egyáltalán a PBR és hogyan lehet ezeket paraméterezni. Néhányat felsorolnék ezek közül:
A szem fényérzékelését a CIE fotometrikus görbe (V(λ)) írja le, ami minden hullámhosszhoz hozzárendel egy [0, 1]-beli súlyt. A görbe a zöld fénynél (555 nm) éri el az 1-et, ez azt jelenti, hogy a szem a zöld fényt látja legjobban (100%-os hatékonysággal). A radiometriai mennyiségekből (Xe) fotometriai mennyiségekbe (Xv) való váltás az alábbi integrállal írható le: 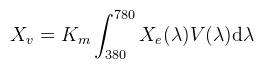
Ahol Km = 683, röviden hívjuk most maximális hatásfoknak (angolul baromi hosszú kifejezés). Ha konyhanyelven akarjuk megfogalmazni, akkor azt lehet mondani, hogy "egy 1 wattos zöld fény fényáramja 683 lumen". Természetesen 3D grafikában megelégszünk egy közelítő képlettel, ami: 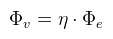
Ahol η a fény hatásfokát jelöli. Ha ez az infó nem áll rendelkezésre, akkor η = 683-at feltételezünk és ekkor a többi mennyiség is így számolható ki. A kérdés, hogy a shadereknek mi legyen a bemenő paramétere: watt vagy lumen? A rövid válasz az, hogy lumen (mert nem foglalkozunk spektrumokkal). A képletek ugyanazok, tehát ha esetleg radianciát írok, akkor nyugodtan lehet érteni helyette fénysűrűséget is. Amivel nem foglalkoznak különösebben az a fények színe. Alapvetően nem is színt kellene mondani, hanem hőmérsékletet (feketetest-sugárzás és társai). A hőmérsékletből RGB színeket előállító képlet bonyolult, de megtalálható itt. A feladat a tükröződési egyenlet analitikus megoldása. Kezdjük a pont fénnyel, mert az a legegyszerűbb, hiszen egyetlen olyan irány van, ahonnan fény érkezhet. Viszont van egy kis gond: mivel nincs területe, a radianciát nem lehet értelmezni. Induljunk ki akkor abból, amit könnyen ki lehet számolni. Jelöljük a pont fény körüli egységgömböt S-el, ekkor a térszögeknél megbeszéltek alapján:
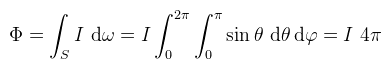
Tehát I-t már ki tudjuk számolni, ami nagyon jó, mert akkor (alkalmazva a korábban felírt képleteket): 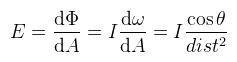
És már csak egy picit kell küzdeni és: 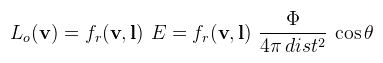
Ez az amit úgy hívnak, hogy inverz négyzet törvény, tehát az irradiancia a fényforrástól való távolság négyzetével csökken. A pont fény általában a pozíciójával és az intenzitásával (I) adott. Vigyázat, az UE4 a fluxust hívja intenzitásnak, ami elég félrevezető! Az inverz négyzet törvénnyel annyi baj van, hogy sosem éri el a 0-t. Ez nem hangzik túl jól, mert optimalizációs célból jó lenne ha a fényeket ki lehetne vágni ha nem látszanak (gondoljunk a forward+ -ra). Ezért a pont fényhez hozzá szoktak venni egy sugarat is és a képlet attenuation = I / dist2 * max(0, 1 - dist / r)-re módosul. A spotlámpa se sokkal nehezebb, hiszen hasonlóan kell gondolkodni, de gömb helyett kúpon vesszük az integrált: 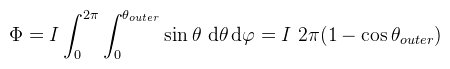
ahol θouter a spotlámpa külső nyitási (fél)szöge. A DICE azt mondja, hogy nekik ez nem tetszik, mert ahogy csökken ez a szög, úgy erősödik az illumináció és ezt a designereknek nehéz kompenzálni. Ezért ők Φ = πI-vel számolnak (én nem). A spotlámpához hozzá szoktak venni még egy paramétert, a belső nyitási szöget (θinner). A két szög között a fény fokozatosan elhalványodik. Ehhez nem írok képletet, ott a kód (meg amúgyis mindenki álmából felébresztve keni-vágja). Gyakran alkalmazott módszer, mert egy egyszerű módja a globális megvilágítás szimulálásának.
De mivel a rücskösség által a felület nem feltétlenül sima, a tükröződési egyenletnek nincs analitikus megoldása. Emlékeztetőül:
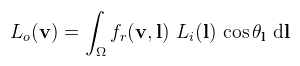
Ahol most Li(l) az environment mapból olvasott érték. Azt mondtam, hogy az integrálra lehet úgy gondolni, mint végtelenül kicsi környezeteken vett összegzésre. Most ez a "végtelenül kicsi" legyen egyszerűen csak "kicsi", tehát osszuk fel a félgömböt egyenletesen N részre és cseréljük le az integrált egy szummára (Monte Carlo integrálás): 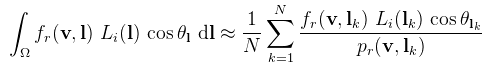
Ahol pr az lk (mint valószínűségi változó) sűrűségfüggvénye (probability density function, PDF). Mivel most egyenletesen osztottam fel a félgömböt, annak a valószínűsége, hogy egy adott pontot választok rajta pr = 1 / 2π. Ahogy egyre nagyobb N-ig megy a szumma, úgy javul a közelítés pontossága is. Ez a képlet a probléma megoldásához jó lesz, az egyenletes eloszlás viszont nem. Mondok egy triviális példát: egy tökéletesen tükröző felület (roughness = 0) egy pontjában egyetlen olyan irány van, ahonnan fény jöhet, tehát bármilyen olyan eloszlás, ami nem ezt az irányt választja, pazarolja az időt. A konvergencia tehát gyorsítható, ha az adott BRDF szerint választjuk meg lk-t és pr-t (importance sampling). Kezdjük először a Lambert-féle BRDF-el: milyen mintavételezési stratégiával gyorsítható a konvergencia? Annyit kapásból észrevehetünk, hogy amikor cos θ = 0, akkor nem jutunk közelebb a megoldáshoz, azaz olyan irányokban fölösleges mintavételezni. Mi lenne ha pr kiejtené cos θ-t, hogy ne is zavarjon? Ehhez pr = (cos θ) / π kellene (a sűrűségfüggvény 1-hez kell integráljon). A levezetést nem írom le, de ennek analógiájára megcsináltam (aki nem hiszi, számoljon utána): CODE
float3 CosineSample(float xi1, float xi2)
{
float phi = 2 * PI * xi1;
float costheta = sqrt(1 - xi2); // mert P(θ) = 1 - cos2 θ
float sintheta = sqrt(1 - costheta * costheta); // mert sin2 x + cos2 x = 1
// PDF = costheta / PI
return float3(sintheta * cos(phi), sintheta * sin(phi), costheta);
}
Tehát ha így választjuk meg az irányt, akkor cos θ is és a Lambert BRDF-ben a π is kiesik. Vigyázat, ez nem jelenti azt, hogy eltűnik a diffúz árnyék! Csak n·l-t cseréltük el úgy, hogy az árnyékos részen egyszerűen nem veszünk mintát! Most akkor valami hasonló kéne a fent bemutatott Cook-Torrance-féle BRDF-re is. Szerencsére ezen se a DICE se az Epic nem veszett össze: CODE
float3 GGXSample(float xi1, float xi2, float roughness)
{
float alpha2 = pow(roughness, 4.0); // eml.: Disney-féle α = roughness2
float phi = 2 * PI * xi1;
float costheta = sqrt((1 - xi2) / (1 + (alpha2 - 1) * xi2));
float sintheta = sqrt(1 - costheta * costheta);
// PDF = (D(h) * dot(n, h)) / (4 * dot(v, h))
return float3(sintheta * cos(phi), sintheta * sin(phi), costheta);
}
Tök jó, ez meg kiejti majd D(h)-t. Megjegyezném, hogy az egyszerűsítéseket célszerű kézzel elvégezni, ugyanis nem nagyon lehet abban bízni, hogy a GPU-n a * (b / b) == a ... Ez már majdnem tökéletes, path tracinghez. Valósidejű megjelenítéshez még mindig lassúcska, mert ahogy a rücskösséget növeled egyre több mintavételezés kell. Azt mondja erre az Epic, hogy: 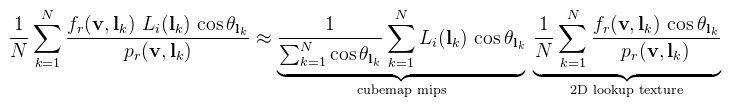
Vigyázat, ez egyébként baromira nem igaz! (lenyeljük) Az Epic felhívja a figyelmet, hogy ez a fajta közelítés az n = v = r feltételezés miatt látható hibákat okoz, például le kell mondani a "megnyúlt" tükröződésekről. Egy 2015-ös jegyzet próbál segíteni ezen, több-kevesebb sikerrel. Az első tagot a cubemap mip szintjeibe számoljuk ki, különböző roughness értékekhez. Ha esetleg realtime kellene előállítani ezt a cubemapet, az sem vészes: ha egyszer lefordult, akkor már gyors (meg nem muszáj N = 2048-ig futtatni; cserébe kicsit zsizsás, amit úgysem veszel észre). Mivel itt konkrétan az irradianciát számoltuk ki, a becsületes neve irradiance cubemap. A második tagot még tovább kell egyszerűsíteni, ugyanis jelenlegi formájában három paramétertől függ (F0, roughness, n·v), tehát legjobb esetben is 3D textúrában lehetne eltárolni. Az F0-tól való függés azonban megszüntethető: 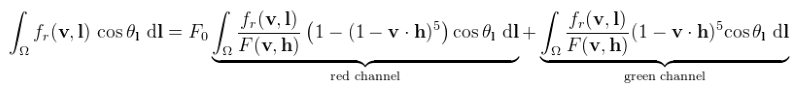
Vigyázat, legalább 16 bites float textúrába kell pakolni, különben nem lesz jó! Ha ezek elkészültek, akkor megjelenítéskor két darab textúra olvasással megúszható az egész buli, ami azért picit hatékony. CODE
float miplevel = roughness * (NUM_MIPS - 1);
float3 r = 2 * dot(v, n) * n - v;
float3 spec_irrad = irradcube.SampleLevel(linearSampler, r, miplevel).rgb;
float ndotv = saturate(dot(n, v));
float2 AB = brdfLUT.Sample(linearSampler, float2(ndotv, roughness)).rg;
color = spec_irrad * (F0 * AB.x + AB.y); // megj.: fémeknél F0 = baseColor
Az előszűrés miatt a cubemap alsóbb mip szintjein seam-ek keletkeznek (pl. minden oldal különböző színű), ennek megoldásához be kell kapcsolni az oldalakon keresztüli szűrést (glEnable(GL_TEXTURE_CUBE_MAP_SEAMLESS)). Hasonlóan lehet gondolkodni a diffúz esetben is, az említett cos mintavételezéssel; ezt még speciel a CubeMapGen is meg tudja csinálni. A neten elérhető egyéb programok, amik papíron tudják a fentit, nem működnek jól. 
Na és akkor mi legyen a sík felületekkel? A DICE azt mondja, hogy oda nem kell textúra, ők helyben raytracelik a tükröződést (a gbufferben). Persze, amikor pont merőlegesen nézel a felületre, akkor nincs semmi információ, úgyhogy ebben az esetben diszkréten eltűnik a tükröződés. Szigetelőknél ez Fresnel miatt nem baj, fémeknél meg lenyelhető béka... Höfö kitalálni egy olyan mintavételezést ami egyszerre segít a diffúz és spekulár eseten is (path tracinghez jól jön). A pontszerű fényekkel könnyű dolgunk volt, mert csak egy irányból jöhetett fény. A területi fények esetében viszont ez már nem igaz, így valamilyen módon muszáj megoldani a tükröződési integrált. Ez a téma még aktív kutatási terület, ezért csak annyit írok róla, amennyit jelenleg meg lehet csinálni.
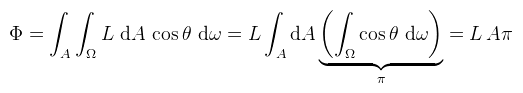
A radianciát egy átrendezéssel megkapjuk. Nézzük most a tükröződési egyenletet. Az envmappal ellentétben a területi fénynél nem szükséges a teljes félgömbön integrálni, hiszen sok helyről nem érkezik fény. Elég tehát a területi fény által bezárt térszögön elvégezni az integrálást, legyen ez Ωlight. Ha így írjuk fel az egyenletet és alkalmazzuk a térszögeknél megbeszélt képletet: 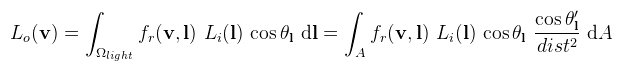
Tehát térszög helyett integrálhatunk a területi fény (felületi) területén. A képlet path tracingben különösen hasznos, mert ezek szerint az importance sampling-ot elvégezhetjük a fényforráson is (explicit light sampling). Ez bizonyos esetekben sokkal gyorsabban konvergál, mintha a BRDF-et mintavételeznéd! Valós időben viszont lassú, és értelmesen nem is lehet előre kiszámolni (túl sok paramétertől függhet). Marad tehát egy közelítő analitikus megoldás és itt kezdődnek a gondok, ugyanis eddig még nem sikerült olyat kitalálni, ami minden esetben jó lenne (különösen az energiamegmaradással vannak bajok). Egy külön nehezítő körülmény, hogy a területi fény részben a pont horizontja alatt lehet. A jelenleg elfogadott megoldásokat levezetés nélkül adom meg. Két fajta területi fénnyel foglalkoztam: (egyoldalú) téglalap és kapszula. A (részben) horizont alatti esetet egyiknél sem kezeltem le, csak annyit csináltam meg, hogy legalább ne világítson a fény olyan helyekre ahova nem kéne (pl. a téglalap mögé). Az összességében igaz, hogy az integrált néhány darab jól megválasztott iránnyal próbálják megoldani (most representative point). Vegyük először a diffúz (Lambert) esetet. Azt mondja a DICE, hogy konstans Li mellett: 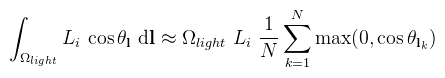
Tehát kellene a térszög és néhány okosan megválasztott lk fényirány. Téglalapra a térszög kiszámolható ennek megfelelően, a választott irányok pedig legyenek (a pontból) a téglalap négy csúcsába illetve a közepébe mutató vektorok. A kapszula egy szakasszal (A, B) és a sugarával (radius) adott. A megvilágítás egy adott p pontban közelíthető úgy, mintha a kapszula egy a pont felé néző téglalap és a ponthoz (a szakaszon) legközelebb eső gömb lenne. Mivel a horizont alatti esetekkel nem foglalkoztam, erre adható egy közelítő képlet: CODE
float DiffuseIlluminanceCapsule(float3 p, float3 n)
{
float illum_rect = ...; // DICE jegyzetéből
float3 closest = ClosestPointOnSegment(p, A, B);
float3 dl = normalize(closest - p);
float dist2 = dot(closest - p, closest - p);
float illum_sphere = PI * saturate(dot(dl, n)) * ((radius * radius) / dist2);
return luminance * (illum_rect + illum_sphere);
}
Nem néz ki tökéletesen, de ez a néhány pontatlanság lenyelhető. 
Ha valaki eddig szúrós szemmel nézett, akkor most még szúrósabban fog nézni, mert a spekuláris tag ennél még egetrengetőbb. Ugyanis GGX eloszláshoz egyelőre nincs elfogadható módszer (Phong-hoz van, na de...), így mindenki az UE4-et másolja. Azt mondják ők, hogy "keresd meg a tükrözött vektorhoz legközelebbi pontot a fényforráson és számolj azzal". Kapszulához van implementáció, de nem kezeli le a horizont alatti esetet, így artifactos. A téglalapot az UE4 meg se csinálja, a DICE meg bevallja, hogy hát nem találtak hozzá megfelelő energiamegmaradási képletet. Szerintem egy ilyen patthelyzetben mondhatom azt, hogy Árnyékokat területi fényekhez is shadow mapping-al lehet csinálni úgy, hogy a fókuszpontot kijjebb tolod és a frustum közrefogja a fényt. Hogy ne kelljen cubemapet használni az ilyen fényeket úgy rakd le, hogy elég legyen egy irányban árnyékot számolni (pl. a Nap ilyen). Korábbi cikkekben is hangoztattam már, hogy mennyire fontos a gamma korrekció. Mostantól viszont nem csak ez kötelező, hanem a tone mapping is (magyarul színleképezés-nek fordítják).

Ezt kompenzálandó a gép úgy menti el a képet, hogy felemeli 0.45-re, így optimálisabban tölti ki a 24 bitet (így lesz a kép sRGB). A visszakonvertálást a monitor végzi el (felemeli 2.2-re). A megvilágításra vonatkozó egyenletek és képletek viszont lineáris értékeket feltételeznek; ez mindaddig nem okoz gondot, amíg hülyeséget számolsz a shaderben (tipp: a PBR nem ilyen). Mit jelent ez OpenGL szempontból? Ha betöltesz egy textúrát és tudod róla, hogy sRGB, akkor olyan formátumot adj meg (GL_SRGB8_ALPHA8). Kivételek a normal map, specular map és hasonlók, mert ezek tipikusan lineárisan vannak tárolva. Másrészt a rajzolás legvégén az egész framebufferre pow(color, 0.45)-öt mondasz (vagy sRGB framebuffert csinálsz, de az nekem sose működik jól). Önmagában viszont nem elég a gamma korrekció, mert amellett, hogy lineáris térben kell dolgozni, a 24 bites korlátot is el kell, hogy felejtsük. A szem érzékelése ugyanis nem 1:256 hanem nagyjából 1:10000 (a valóság ennél még nagyobb). Ezt hívják high dynamic range-nek; ha pontosan akarjuk modellezni a valóságot, akkor legalább ilyen precízióban kell tárolni a kirenderelt képet (ARGB16F vagy A2R10G10B10 elég). Amit persze végül vissza kell képezni a backbuffer 24 bitjébe, ezt csinálja a tone mapping. Ha nem teszed ezt meg, akkor már egy 40 W-os villanykörte is kiégeti a képet. Mutatom inkább: 
Ha tehát egy engineben beállítasz egy fényt és a bal oldalihoz hasonló képet kapsz, akkor az nem azt jelenti, hogy a fényed intenzitását kell csökkenteni, hanem hogy az engine nem tone mappel. Amit itt elmondtam az részletesebben elolvasható az Uncharted 2 prezentációjában (és maga a tone mapping függvény is). Kell viszont még egy harmadik dolog is, amit expozíciónak hívnak (exposure). A szem ugyanis folyamatosan adaptálódik a beérkező fénysűrűséghez: egy sötét szobában a pupilla kitágul, így több fényt enged be. Ha innen kimész a napfénybe, akkor a pupilla azonnal összeszűkül, de egy rövid ideig még nem látsz semmit, mert a retina lassabban adaptálódik a megváltozott fényviszonyokhoz, így esetleg felrúgod a macskát. Ezt is fontos szimulálni, különben a 40 W-os villanykörte mellett egy másik szoba túl sötétnek látszódhat és kínodban megint elkezdesz hackelni. Ez utóbbi az, amivel picit kell foglalkozni. Először is vegyél egy (digitális) fényképezőgépet (tipp: a mobilodban jó eséllyel van) és próbálj meg lefotózni valamit. A gép automatikusan elvégzi az expozíciót, ami három dologtól függ (részletesen itt):
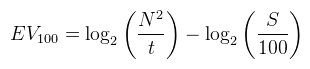
Választhatsz, hogy a három paramétert beállítod kézzel (erre léteznek módszerek, például a Sunny 16 szabály), vagy pedig megcsinálod (fél)automatikusra. Utóbbi esetben a fényképezőgéphez hasonlóan egy fénysűrűség mérést kell elvégezni, például Erik Reinhard módszerével: 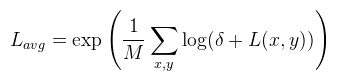
Ahol M a pixelek száma, δ pedig egy pici érték a szingularitás elkerüléséhez. Ezt a klasszikusnak mondható módszerrel valósítottam meg, tehát egy 64x64-es textúrába átlagoltam a képet (elvégezve a log-ot), majd ezt átlagoltam tovább 16x16, 4x4 és végül 1x1-be, ezen utolsó lépésben végezve el az exp-et. Ebből az expozíciós érték a következőképpen kapható meg (S = 100): 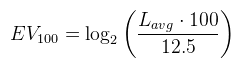
Az expozíció pedig a DICE levezetésének megfelelően: 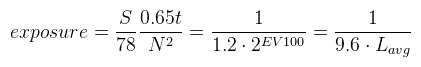
Tonemap előtt a fénysűrűséget felszorozva ezzel automatikusan adaptálódik a kép. Ezt az adaptációt az eddig megszokott módon lehet késleltetni (ld. korábbi cikkem). A fejlesztés eredménye végül három program lett. Egy irradiance cubemap generátor (DX10), egy egyszerű realtime path tracer (DX10) és egy bonyolultabb OpenGL 3.2-es demó. Path tracingről majd külön cikket fogok írni, úgyhogy arról nem mondok most semmit. OpenGL-hez a core profile fontos, mert sok PBR-hez szükséges dolog része lett a szabványnak.
Mitől fizikán alapuló egy megjelenítő? A pongyola válasz az, hogy fizikailag korrekt, de nem feltétel, hogy fotorealisztikus legyen. Azonban a mainstream enginek közül van amelyik azt állítja magáról, hogy PB, de mégsem teljesen az. Leveleztem erről a DICE egyik fejlesztőjével és szerinte három olyan dolog van, amit teljesíteni kell ahhoz, hogy egy engine PB legyen:
Az Unreal 4 már lényegesen jobb, de a fények paraméterezése el van rontva. Például a spot fény állításuk szerint lumenben várja az értéket, ehhez képest 1700 lumen alig világít meg egy 36 négyzetméteres szobát (auto exposure-t direkt kikapcsoltam). A hiba valószínűleg abból adódik, hogy centiméterben számolnak, pedig méterben kellene... A DICE-féle Frostbite mindhárom dolgot implementálja, de ezt nem sikerült kipróbálnom. A CryEngine 3-at szintén nem. Offline rendererek közül a könyvhöz tartozó pbrt (nem próbáltam) és az azon alapuló Mitsuba helyesen implementálja a dolgokat, így összehasonlítási alapnak az utóbbit használtam. Zárszónak annyit, hogy ez a technológia nagyon is aktuális és még mindig fejlődés alatt áll (pl. a területi fények jobb analitikus közelítése). Véleményem szerint a hardver fejlődésével egyre többször fog előkerülni a Monte Carlo integrálközelítés, így végső soron a realtime path tracing felé haladunk. Kód a szokott helyen, akiknek nincs számítógépe azoknak meg videó. Höfö:
Irodalomjegyzék https://seblagarde.files.wordpress.com/... - Moving Frostbite to Physically Based Rendering (DICE, 2014) http://www.crytek.com/download/2014_03_25_CRYENGINE_GDC_... - The Rendering Technology of Ryse (Crytek, 2014) http://blog.selfshadow.com/publications/s2013-shading-course/karis/... - Real Shading in Unreal Engine 4 (Epic, 2013) http://blog.selfshadow.com/publications/s2013-shading-course/hoffman/... - Physics and Math of Shading (Naty Hoffman, 2013) http://www.crytek.com/download/fmx2013_c3_art_tech_... - The Art and Technology behind Crysis 3 (Crytek, 2013) https://mediatech.aalto.fi/~jaakko/T111-5310/K2013/... - Reflectance Equation, Rendering Equation (Aalto University, 2013) http://blog.selfshadow.com/publications/s2012-shading-course/burley/... - Physically Based Shading at Disney (Disney, 2012) http://renderwonk.com/publications/s2010-shading-course/... - Practical Implementation at tri-Ace (tri-Ace, 2010) http://www.pbrt.org/ - Physically Based Rendering From Theory to Implementation (2010) |
