|
Nem lehet szó nélkül elmenni a 20. század hivatalosan is megválasztott (rangsorban nyolcadik) legjelentősebb algoritmusa mellett, ami gyors Fourier transzformáció névre hallgat (kiejtés: furié). Valamilyen oknál fogva ez kimaradt az egyetemi éveimből, holott csak a felhasználásait tekintve is forradalminak számít. Jelfeldolgozástól kriptográfiáig rengeteg területen használják; természetesen ezen viszonylag széles skálából most a számítógépes grafikában való alkalmazásairól fogok írni, konkrétan a valósidejű óceán megjelenítésről.
Lektorálta: Bálint Csaba
Tartalomjegyzék
Aki úgy gondolja, hogy eleget tud a komplex számokról, az átugorhatja ezt a bekezdést. Történelemleckeként annyit, hogy már az ókori görögöknél (Hérón) is felmerültek olyan problémák, ahol negatív számok gyökét kellett volna meghatározni, de mint ahogy az irracionális számok koncepcióját, úgy ezt is kihajították a...Musaeum ablakán...
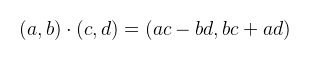
Ezzel a definícióval élve, ha vesszük a (0, 1) komplex szám önmagával vett szorzatát (négyzetét), akkor meglepő módon (-1)-et kapunk. Jelüljük az említett komplex számot i-vel (fizikusok j-vel), ekkor egy tetszőleges komplex szám 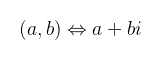
alakban írható, ahol a és b valós számok, és a-t a komplex szám valós részének, b-t pedig a képzetes részének nevezzük. A jobb oldali jelölés előnye, hogy a valós számokból ismert képleteinket ugyanúgy alkalmazhatjuk, nem elfelejtve, hogy i2 = -1. A továbbiakban ezt a fajta jelölést fogom használni (bár megemlíteném, hogy papíron az előbbi időnként kényelmesebb). Amiért ez megtehető, az azzal indokolt, hogy a komplex számok halmaza is ún. (szám)testet (field) alkot a fent bemutatott szorzással, illetve a tagonként vett összeadással. A műveletek kommutativitása, asszociativitása, disztributivitása illetve invertálhatósága némi belegondolással levezethető. Egy olyan művelet van, amit valós számoknál nem használunk, ez a konjugált: 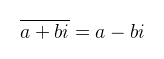
A konjugáltat *-al is szokták jelölni; későbbi bekezdésekben én is ezt fogom használni (tipográfiai szempontból átláthatóbb). Jogosan merül fel a kérdés, hogy vajon a komplex számok halmaza izomorf-e a 2D vektorokkal? Ameddig halmazként tekintünk rájuk, addig igen, a műveleteket figyelembe véve viszont értelemszerűen nem. Természetesen ez nem akadályoz meg senkit abban, hogy komplex számokat helyvektorokként vizualizáljon, különösen amikor az ún. n-edik komplex egységgyökökről van szó (zn = 1). Ezeknek a (diszkrét) Fourier transzformációval való kapcsolatáról majd később írok. Első példaként határozzuk meg a 4x2 + 1 = 0 egyenlet gyökeit. Az általános iskolában tanult másodfokú egyenlet megoldóképlete alapján a diszkrimináns -16, amire akkor azt mondtuk, hogy az egyenletnek nincs (valós) megoldása. Felvértezve azonban a komplex számokkal √(-16)-ből kiemelhetünk i2 = -1-et, így ±i/2-t kapva egyszerűsítés után. Ezek után megfogalmazható az algebra alaptétele, miszerint minden n-edfokú polinomnak pontosan n darab gyöke van (multiplicitást is beleértve). A témához kapcsolódóan két probléma foglalkoztatta a 18. század vezető matematikusait: a rezgő húr probléma (d'Alembert, Euler, Bernoulli), illetve a hővezetés egyenlete (Fourier).
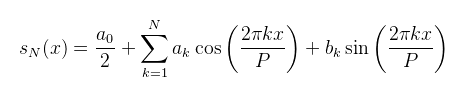
összeget, ahol 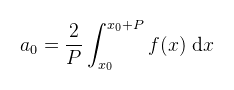
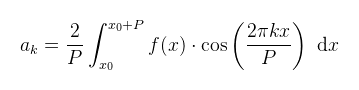
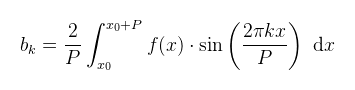
(megj.: sN(x) nem a legszerencsésebb jelölés, de ennek megindoklása csak tovább bonyolítaná a cikket) Ha N helyére végtelent írunk, akkor az így kapott kifejezés az f függvény Fourier sora. Felmerül a kérdés, hogy a sor milyen feltételek mellett konvergens (azaz N → ∞ esetén mikor és hogyan állítja elő a függvényt). A válasz az, hogy "attól függ milyen függvény", illetve "attól függ milyen konvergencia". Ez a harmonikus analízis témaköre, ami elég körültekintően kivesézi az egyes eseteket, de ehhez a cikkhez csak néhány egyszerűbbet említek meg:
Más okból is célszerű legalább L2-beli függvényeket választani, ugyanis az előbb említett feltétel p = 1 esetén nem igaz (értsd: nem elég, hogy a függvény "csak" integrálható). Konstruálható például olyan tisztán L1-beli függvény, aminek a Fourier sora divergál. De inkább nézzük meg egy példán keresztül, hogy mire lehet számítani. Vegyük mondjuk a fűrészfog függvényt, amit az egyszerű f(x) = x - floor(x) képlettel lehet leírni (egyébként meg pl. szintetizátorok használják hangelőállításra). A függvény P = 1 szerint periodikus, illetve a [0, 1] intervallumon integrálható, itt ugyanis elég úgy kezelni, mintha a g(x) = x függvény lenne. Az eredményt N = 4 és N = 16-ra mutatom: 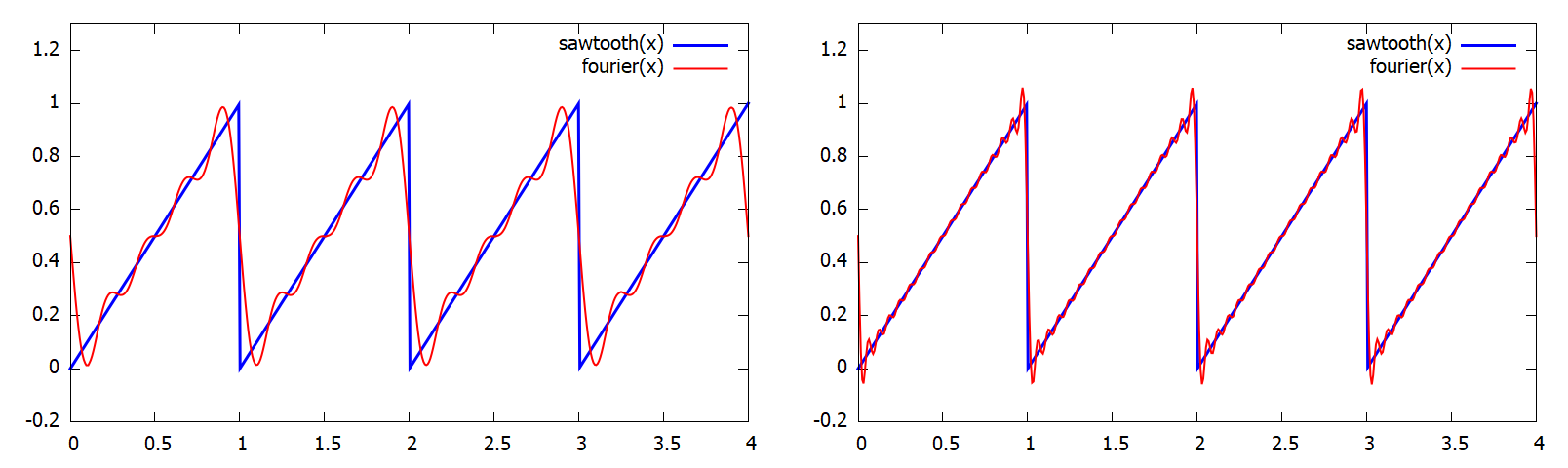
Ilyet már láttunk, amikor például convolution shadow map-et simítottunk el a Fourier sora segítségével. Mivel a fűrészfog függvény páratlan (f(-x) = -f(x)), az ak együtthatók mind nullák, a CODE
A0 = 0.5
b(k) = -1 / (pi * k)
sN(x) = A0 + sum[k=1:N] b(k) * sin(2*pi*k*x)
Mint mondtam, shadow mapping-ben már láttuk egy gyakorlati alkalmazását a Fourier soroknak, de jogos a kérdés, hogy általános esetben miért jó egy ehhez hasonló előállítás (már ha az nem elég, hogy a rezgő húrt illetve a hővezetés egyenletét leírja). Mivel szinusz/koszinusz függvények összegéről van szó, a sor kapásból teljesít egy rakatnyi hasznos tulajdonságot (pl. végtelenszer folytonosan differenciálható), amik által az eredeti függvény bizonyos viselkedéseit/tulajdonságait is meg lehet jósolni (és ez a méréselméletben különösen hasznos, ami által eljutunk majd az óceánfelület analitikus modelljeihez). Utolsó megjegyzésként, ha a fenti Fourier röf definíciót gondolatban szétbontjuk, akkor az vehető észre, hogy az egyes tagok frekvenciái az f0 = 1/P alapfrekvencia, pontosabban az ω0 = 2π/P alap körfrekvencia egész számú többszörösei. A szumma így előálló k-adik tagját nevezzük k-adik felharmonikusnak. Az egyik részcél az lesz, hogy (megint konyhanyelven) a "sütiből előállítsuk a receptet". Ez matematikailag azt jelenti, hogy valamilyen (analóg vagy digitális) jelből meghatározzuk az egyes felharmonikusok amplitúdóit és fázisait a frekvencia függvényében. Az így kapott diagramo(ka)t nevezzük spektrumnak. (megj.: egyéb irodalmak esetleg máshogy értelmezik a spektrum fogalmát, illetve korábban említettem, hogy egy mátrix sajátértékeit is szokás spektrumnak hívni; későbbi bekezdésekben majd kiderül, hogy van-e kapcsolat a kettő között) A fenti felírás egyik problémája, hogy két (látszólag) különböző Fourier együttható van, amiket nem is mindig trivi kiszámolni. Célszerű lenne egy olyan alakban felírni a Fourier sort, hogy csak egy darab együttható legyen, ami cserébe viszont komplex. A fázist is szemléletesen lehet vizualizálni egy ilyen alakban, mint a komplex együttható és a valós számtengely által bezárt szöget. Az átíráshoz induljunk ki az Euler formulából:
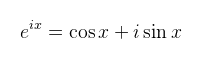
Ha megnézzük a jobb oldalt, az a korábban már látott felírása egy komplex számnak, ami alapján a koszinusz felírható az eix valós részeként, a szinusz pedig a képzetes részeként. Ha hasonló módon felírjuk az Euler formulát e-ix-re is, akkor a kapott két egyenletet összeadva illetve kivonva kapjuk, hogy: 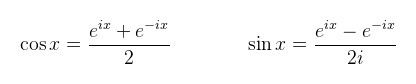
Mielőtt ész nélkül behelyettesítenénk ezeket a fenti Fourier sor definícióba, érdemes alkalmazni a már említett körfrekvencia képletet (ω = 2π/P), amivel kicsit érthetőbben lehet felírni az átalakításokat: 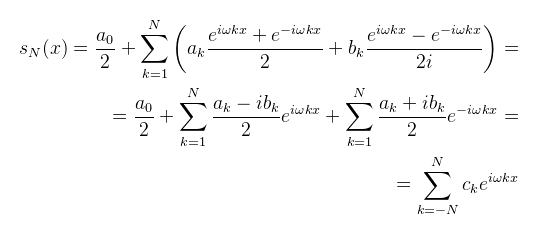
Höfö ellenőrizni, hogy nem számoltam-e el (tudom, hogy ez is röf, de nem röfögök most már többet; ez nem elszámolás hanem elírás). A ck együtthatók a következőképpen írhatóak fel kompaktabb alakban: 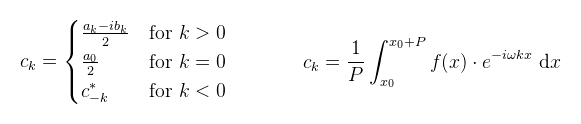
Remélem senki sem siklott át azon tény felett, hogy (mint említettem) a konjugáltat *-al jelölöm, másrészt, hogy az új szumma -N-től N-ig megy. Emiatt megjelentek negatív körfrekvenciák is a képletben, ami nem egy létező jelenség, hanem ennek a felírásnak egy tulajdonsága. Mivel a negatív/pozitív körfrekvenciákhoz tartozó értékek egymás konjugáltjai, összeadva őket az eredmény valós lesz. A további magyarázkodások elkerülése végett itt írom le, hogy egy adott felharmonikus amplitúdója megkapható a ck komplex szám hosszaként, a fázisszög pedig a képzetes és valós rész hányadosának arkusz tangenseként. Egy pillanatra felejtsük el a "diszkrét" szót, és nézzük meg, hogy konkrétan hogyan néznek ki a felharmonikusok, illetve az (amplitudó)spektrum. Példának továbbra is jó lesz a fűrészfog függvény Fourier sora.
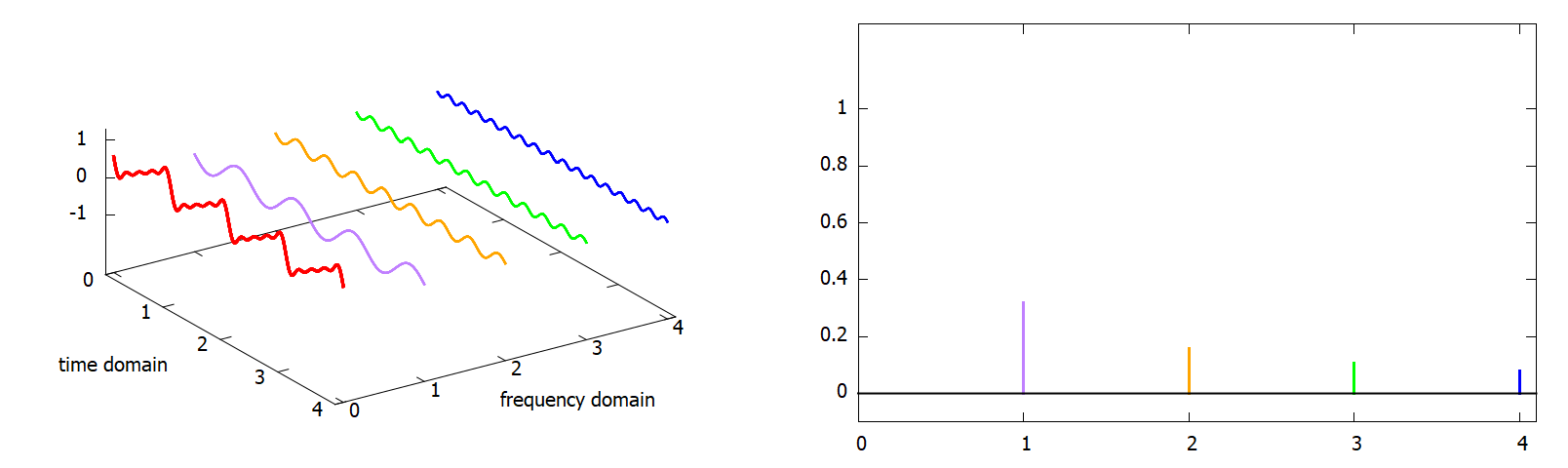
A bal oldali ábrán látható pirossal az eredeti Fourier sor (most mint jel), illetve annak felharmonikusai (amiket összeadva előáll). Amikor arra vagyunk kíváncsiak, hogy egy időtartománybeli jel tartalmaz-e egy adott frekvenciát, azt a frekvenciatartományba való transzformálásával tudjuk ellenőrizni. A jobb oldali ábra ezt a frekvenciatartománybeli felírást mutatja, mint az egyes felharmonikusok amplitúdóit. (megj.: itt most az f0 = 1 alapfrekvencia alapján rajzoltam meg a diagramot, de nyilván körfrekvenciára is teljesen hasonló) A frekvenciatartományba való átalakítást írja le a Fourier transzformáció analóg (folytonos) jelekre, illetve a diszkrét Fourier transzformáció (DFT) digitális (mintavételezett) jelekre. Tegyük fel, hogy felvettünk valamilyen zenét, viszont valami interferencia miatt egy magas frekvenciájú sípolás került a felvételbe. Ilyenkor a spektrum előállításával ez megtalálható, eltüntethető, és egy inverz Fourier transzformációval megkapjuk a javított zenét. A továbbiakban a DFT-vel fogok foglalkozni, mert a gyakorlatban ez dominál (a gép ezzel tud dolgozni). A definíció valamilyen {x[0]...x[N-1]} minták sorozatára (k ∈ [0, N - 1]): 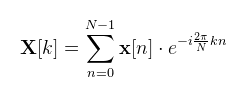
A DFT tehát egy {x[k]} valós vagy komplex sorozatot alakít át az ugyannyi elemű {X[k]} komplex sorozatba. A műveletigényére ebből rögtön meg is mondható, hogy négyzetes (Ο(N2)). A másik amit észreveszünk, hogy felírható mátrix-vektor szorzásként is. Milyen transzformációkat is írtunk le mátrixokkal? Például lineárisakat (és valóban, ez egy lineáris transzformáció). Emellett invertálható is: 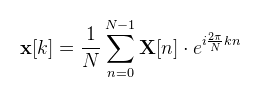
Különféle irodalmak különféle helyekre teszik az N-el való osztást; ennek megvan a magyarázata, de a fenti példából kiindulva világos lesz, hogy most a DFT-be kell az osztás és nem az inverzébe. Egyelőre vegyünk egy 2-periódusú szinusz hullámot. Ha jól számoltuk ki a DFT-t (N = 32 mintára), akkor a 0.5 alapfrekvenciában kell megkapjuk a hullám amplitúdóját (ugyanúgy a megfelelő X[k]-k hosszát véve): 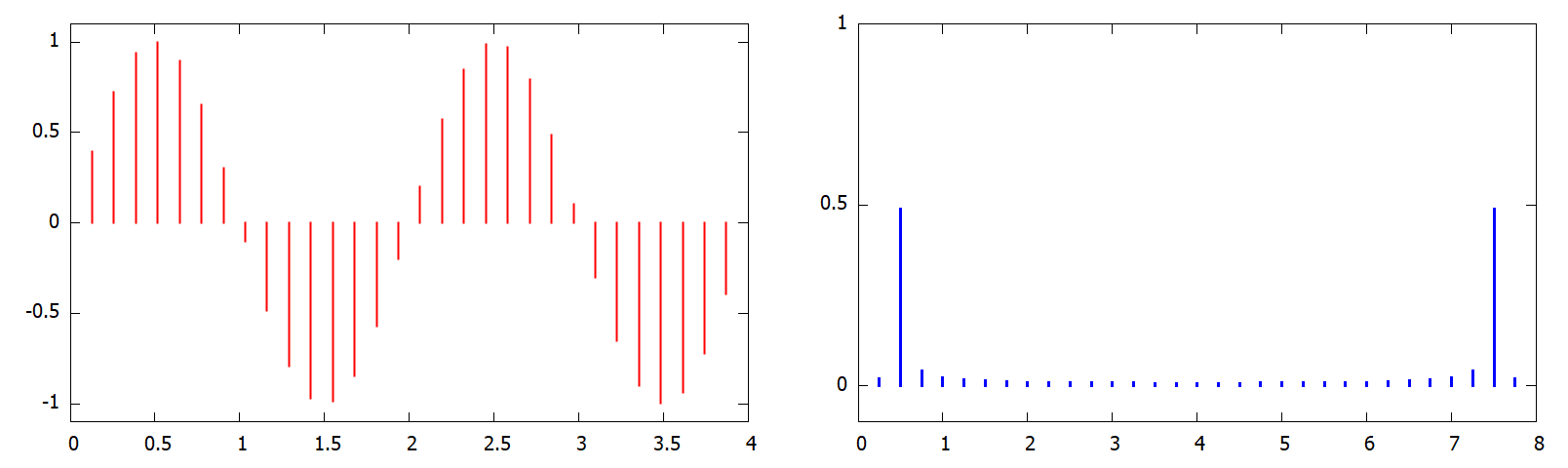
(megj.: az említett negatív körfrekvenciák miatt kétszer kaptuk meg. A DFT-nek tehát csak az első N/2 tagja hordoz tényleges információt) Egy kicsit arról, hogy hogyan is készítettem el az ábrákat. A bal oldal azt mutatja, hogy 4 másodpercig mintavételeztem, összesen 32 mintát, azaz a mintavételezési frekvencia 8 minta/másodperc. Innen a mintavételi időtartam h = 1/8 másodperc. A frekvenciatartomány lépésközét ebből lehet meghatározni a Δf = 1 / (N*h) képlettel. Az is feltűnő, hogy a spektrum az említett helyeken kívül is nemnulla; ez a Fourier transzformáció egy "tulajdonsága", hogy gyakran Dirac delta függvényekkel fejezzük ki az eredményt (konyhanyelven "az ott valójában egy függőleges vonal, gyökér"). Néhány mondat a mintavételezésről: világos, hogy ha magas frekvenciákat tartalmazó jelet nem elég sűrűn mintavételezünk, akkor teljesen más eredményt kapunk, mint kellene (aliasing). A Nyquist mintavételezési tétel azt mondja, hogy a mintavételezési frekvencia nagyobb kell legyen a jel legmagasabb frekvenciájának kétszeresénél (Nyquist rate). A mintavételezési frekvencia fele (Nyquist limit) azt a maximális frekvenciát jelenti, amit még reprezentálni lehet. Például a CD lemeznek 44 kHz a mintavételezési frekvenciája, azaz legfeljebb 22 kHz-es felhangokig tárolja a felvett zenét. (megj.: nem ez a baj vele, mert ennél magasabb frekvenciákat úgysem hallunk, hanem az, hogy az egyes minták 16 biten vannak tárolva, emiatt az elég nagy amplitúdókat levágja. Ha ezt kompenzálják, akkor pedig az apró részletek nem lesznek hallhatóak. Ez pontosan ugyanaz a probléma, mint grafikában az LDR vs. HDR) Mint mondtam a DFT Ο(N2) komplex szorzás-összeadás párossal számolható ki, ami elég lassú (amennyiben részletes óceánfelületet szeretnénk majd megjeleníteni). Ordít viszont róla, hogy egy compute shader segítségével közel lineáris időre hozható: CODE
shared vec2 values[N]; // { x[k] }
layout (local_size_x = N) in;
void main()
{
int k = int(gl_LocalInvocationID.x);
// x[k] értékek betöltése
values[k] = imageLoad(readbuff, k).rg;
barrier();
// DFT kiszámolás
vec2 result = vec2(0);
for (int n = 0; n < N; ++n) {
vec2 coeff = values[n];
float theta = (TWO_PI * n * k) / N;
float cos_t = cos(theta);
float sin_t = sin(theta);
result.x += coeff.x * cos_t + coeff.y * sin_t;
result.y += coeff.y * cos_t - coeff.x * sin_t;
}
// eredmény kiírása
imageStore(writebuff, k, vec4(result, 0, 0));
}
A 60-as évek matematikusai kezüket-lábukat adták volna egy ilyen megoldásért, de mivel akkor még a GPU sem létezett, kénytelenek voltak más módszerekkel gyorsítani. Kissé meglepő, hogy ezt az algoritmust Gauss is feltalálta a 19. század elején, de több szerencsétlen ok miatt nem terjedt el széles körben, ezért elfelejtődött. Az algoritmus újrafeltalálása James Cooley és John Tukey 1965-ös dolgozatában történt meg, így nem túl meglepő módon az egyik megoldást Cooley-Tukey FFT algoritmusnak hívják (de még ezen belül is van több változata).

Ami alapján a kétpontos DFT: 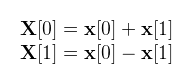
Ezt hívják pillangó műveletnek és az alábbi folyamatábrával szokás vizualizálni (nem írtam el): 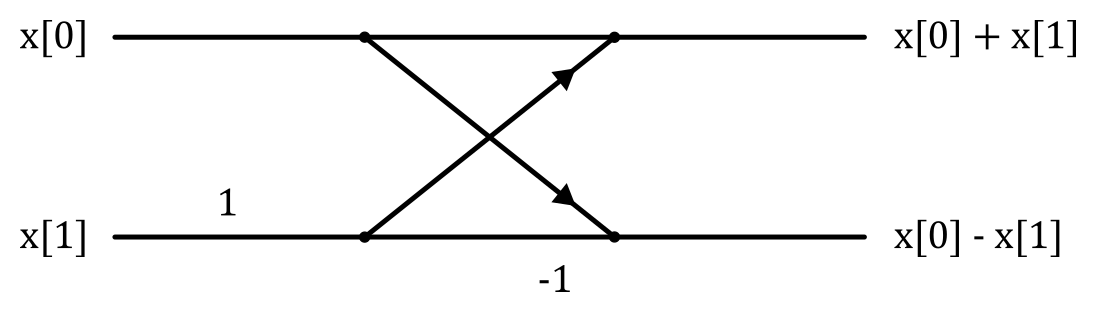
Egy általános pillangó művelet valamilyen a, b, α ∈ ℂ értékekre az a + αb és az a - αb értékeket adja meg. Az ábrán α = 1, ahogy az előbb kiszámoltam (egyébként majd az ún. twiddle factor fog odakerülni), az alul levő -1 pedig szintén az előbb kiszámolt e-iπ (ez mindig -1 lesz). Lépjünk tovább a négypontos DFT-re (és ennél tovább nem is fogok menni, mert nehéz megrajzolni a pillangó diagramokat). Hasonlóan mint előbb, kihasználva, hogy N = 4: 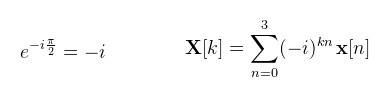
Amit kifejtve kapjuk, hogy: 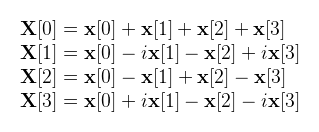
És átrendezésekkel alakítsuk át pillangó műveletekké: 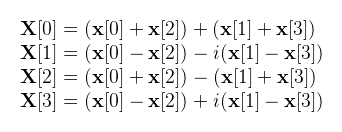
Ha összeszámoljuk ez összesen 4 darab pillangó művelet, tehát 8 darab komplex szorzás és összeadás (16 helyett). Az FFT ezek szerint úgy gyorsítja az algoritmust, hogy egyszerű manipulációkkal újrafelhasználja a már kiszámolt részeredményeket. Lássuk ennek a számolásnak a diagramját (figyeljétek bal oldalt az indexeket!): 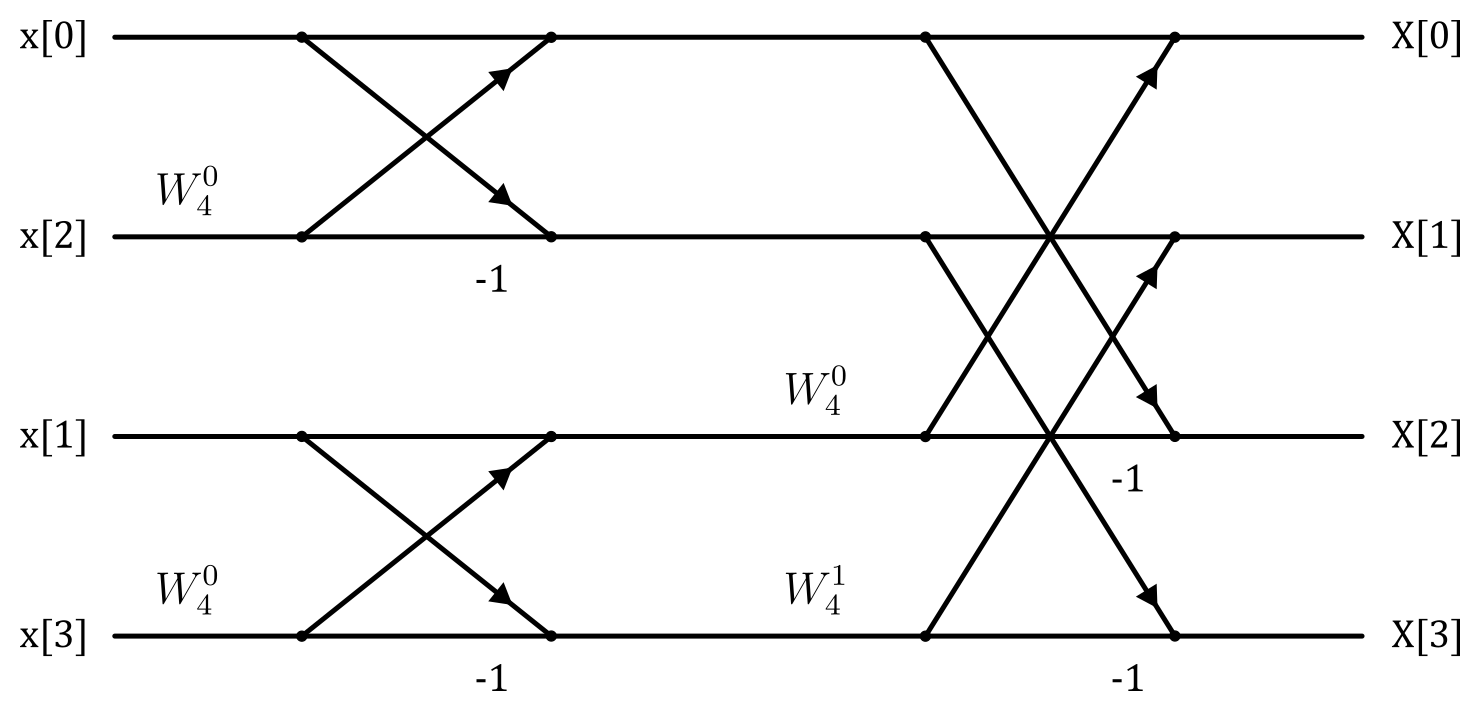
Oké, szóval az átrendezések miatt a kiinduló sorozatot is át kell rendezni, de ha jobban megnézzük, ez az indexek bitjeinek megfordításával megtehető (és erre van beépített függvény GLSL-ben). Ezen kívül az ábrán most már a twiddle factor-ok általános jelölését használtam: 
Amik egyébként az N-edik komplex egységgyökök és ráadásul N szerint periodikusak, így előre ki lehet őket számolni (emiatt szoktak nagyobb radixokkal dolgozni). Egy kicsit matematikaibb oldalról megközelítve, az FFT szétbontja a DFT-t a páros illetve páratlan indexű tagjaira, ami általánosan felírva (a páratlan szummából kiemelve a twiddle factor-t): 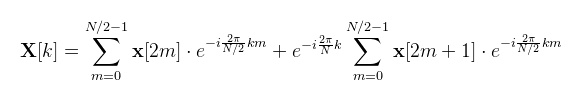
Az említett periodicitás miatt pedig: 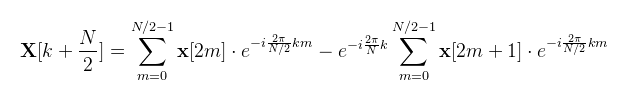
A kettő együtt láthatóan egy pillangó művelet. Ha ugyanezt a szétbontást rekurzívan eljátsszuk a bal és jobb oldali szummákra, akkor log2N lépés után már a kétpontos DFT-t kapjuk. A legintuitívabb implementáció tehát a rekurzió. De mint tudjuk, shader-ekben nincs olyan, szóval egy iteratív megoldást kellene találni. Először megmutatom a wikipédián is megtalálható implementációt, felkommentezve (a bejövő adatot eleve az X[k] tömbbe rendeztem át, így csak azt fogom módosítani): (megj.: pillangó csoport alatt az egymást keresztező pillangó műveletek halmazát értem) CODE
// minden függőleges szakaszra (s) a pillangó diagramon
for( int s = 1; s <= log2_N; ++s ) {
int m = 1 << s; // pillangó csoport magassága
int mh = m >> 1; // pillangó csoport magasságának fele
// első m-edik komplex egységgyök
float theta = GL_2PI / m;
Complex W_m(cosf(theta), -sinf(theta));
// m soronként jön a következő pillangó csoport
for( int l = 0; l < N; l += m ) {
// twiddle factor kezdőérték (k = 0)
Complex W_m_k(1, 0);
// minden pillangóra ebben a csoportban
for( int k = 0; k < mh; ++k ) {
Complex u = X[l + k];
Complex t = W_m_k * X[l + k + mh];
// pillangó művelet
X[l + k] = u + t;
X[l + k + mh] = u - t;
// növeljük a hatványt
W_m_k = W_m_k * W_m;
}
}
}
(megj.: a jelölés ne zavarjon össze senkit; ez értelemszerűen nem ugyanaz az m és k, mint a képletben!) Igen, ebben az algoritmusban vannak olyan dolgok, amiket nem magyaráztam el, például hogy az egyes szakaszokban lehet használni kisebb komplex egységgyököket is (számoljatok utána, ugyanaz fog kijönni). Emellett helyben végzi el az FFT-t, mint mondtam azzal az előfeltétellel, hogy a tömb már át van rendezve. A valódi ok, amiért ezt az algoritmust megmutattam az, hogy némi módosítással triviálisan átírható compute shader-be. Ehhez a két belső ciklust (ami ha kiszámoljátok szakaszonként N/2 pillangó műveletet végez el) kellene egyesíteni egy darab ciklusba, ami viszont N műveletet végez el (amivel mellesleg nyilvánvalóbb is az Ο(N log2N) műveletigény). Ez persze némi redundanciát jelent majd, de bőven meg fogja érni. Gondoljuk akkor végig, hogy hogyan lehetne ezt megcsinálni. Az első logikus dolog, hogy a twiddle factor-t ne ciklussal számoljuk ki, hanem egy lépésben (és akkor a diagramra/képletre is jobban fog hasonlítani). A fenti algoritmus, mint mondtam egy adott szakaszra csak egyszer végzi el ugyanazt a pillangó műveletet; ez most meg fog változni annyira, ahányszor szerepel az eredeti felírásban. Ki kell számolni tehát, hogy egy adott szakaszban (redundanciát is figyelembe véve) hol kezdődnek a pillangó műveletek. Ha ez megvan, akkor az előző szakasz eredményéből lehet kiszámolni az aktuális értékeket (azaz kell plusz egy tömb, a számolásokat pedig az eredeti és eközött pingpongoztatom el a jobb oldalig). Nézzük meg a kódot, érthetőbb: CODE
Complex T[N];
Complex (*pingpong[2])[N] = { &X, &T };
int src = 0;
// minden függőleges szakaszra (s) a pillangó diagramon
for( int s = 1; s <= log2_N; ++s ) {
int m = 1 << s; // pillangó csoport magassága
int mh = m >> 1; // pillangó csoport magasságának fele
// redundanciát is figyelembe véve
for( int l = 0; l < N; ++l ) {
int k = (l * (N / m)) & (N - 1);
int i = (l & ~(m - 1)); // pillangó csoport kezdő sora
int j = (l & (mh - 1)); // pillangó index a csoportban
// WNk ahogy fent leírtam
float theta = (GL_2PI * k) / (float)N;
Complex W_N_k(cosf(theta), -sinf(theta));
Complex u = (*pingpong[src])[i + j];
Complex t = W_N_k * (*pingpong[src])[i + j + mh];
// pillangó művelet
(*pingpong[1 - src])[l] = u + t;
}
// tömb csere
src = 1 - src;
}
Egy kis magyarázat: ha tudjuk, hogy a maradékos osztó kettőhatvány, akkor pozitív számokra a % m == a & (m - 1); ebből némi számolással levezethető, hogy miért a megfelelő értékeket kapjuk az indexekre. Mivel az FFT kettőhatvány méretű sorozatokon dolgozik, az eredmény garantáltan az X tömbben lesz. Ha esetleg az elemek száma nem kettőhatvány, akkor ki kell egészíteni az eredeti tömböt nullákkal. Ezt a módosított algoritmust már könnyedén át lehet írni compute shader-be, amiben a belső ciklus eltűnik, a ciklusváltozót (l) pedig megkapjuk a gl_LocalInvocationID változóból (ugyanúgy, mint fent a DFT-nél). Ezzel a műveletigény közel log2N lesz, azaz például egy 1024 hosszú mintasorozatra 10 lépésben (!) kiszámolja a DFT-t. A kódot most még nem írom le (bár nem kell hozzá nagy fantázia), majd a konkrét óceán spektrumok (inverz) transzformációjánál. (megj.: nem tudom észrevettétek-e, hogy a pillangó műveletből eltűnt u - t, így műveletigényben majdnem ugyanolyan gyors ez is, mint az előző. Höfö rájönni, hogy miért :) Annyit segítek, hogy a twiddle factor-ral kapcsolatos) A matematikai háttérrel felvértezve térjünk át az óceánfelület modelljeire. Ezt a tudományágat tengertannak vagy fizikai oceanográfiának nevezik. Ebbe beletartozik a hullámok viselkedésének vizsgálata, illetve a fény-óceán interakció is (de utóbbiba nem megyek bele részletesen).

Ahol k a hullámvektor hossza (kapcsolata a hullámhosszal: k = 2π / λ), t az idő, ω pedig a (kör)frekvencia, aminek a kapcsolatát a hullámvektorral az ún. diszperziós reláció írja le. Ez láthatóan egy viszonylag egyszerű modell, nincs is túl sok köze a valósághoz, viszont több ilyen összekombinálásával elő lehet állítani többé-kevésbé hihető vízfelületet, például ha a célhardver nem elég erős a komplikáltabb módszerekhez. A diszperziós reláció más lehet attól függően, hogy milyen vízfelületről van szó. Két dolog befolyásolja: a víz mélysége (D), illetve a felületi feszültség (ez most nem érdekes). Az általános képlet 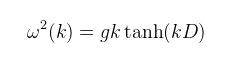
ahol g = 9.81 m/s2 a gravitációs konstans. Amennyiben a szóban forgó víz elég mély, akkor a hiperbolikus tangens eltűnik (gondolatban felrajzolva kD = 3-tól már nyugodtan tekinthető 1-nek). A megjelenítés szempontjából is célszerű mély óceánnal foglalkozni, mert akkor nincs szükség fénytörés számolásra (amiről tudjuk, hogy problematikus ilyen jellegű felületeknél). Dióhéjban a Gerstner modellel az a gond, hogy nem trivi elérni vele, hogy periodikus legyen (megoldható, de mivel eleve nem realisztikus, fölösleges vacakolni). Persze ez inkább 3D-ben jelent problémát, 2D-ben nyugodtan lehet használni, sőt fel is adom höfönek, hogy csináljatok egy egyszerű 2D játékot, amiben ilyen hullámok vannak. Addig is ez kuka, térjünk át a statisztikai alapú modellre. Erről azt kell tudni, hogy az óceánfelület magasságát valószínűségi változóként kezeli, az oceanográfiából származó eredmények pedig kimutatták, hogy ezek a magasságok következetesen a normális (Gauss) eloszlást követik. Az analitikus modellek építéséhez szükséges adatokat a hullámok magasságának mintavételezésével szerzik meg, pl. bójákkal, radarral vagy egyszerűen csak megfigyeléssel. Ha valakit mélyebben érdekel a mérés menete, illetve az adatokból előálló spektrum, akkor itt egy rövid összefoglaló. Most viszont analitikus modellt keresünk, ami lehetőleg minél jobban közelíti a mért adatokat. Ez hasonlóan mint előbb, az óceánfelület magasságának szinusz illetve koszinusz függvényekre bontásán alapul, és az alábbi képlet írja le (ami láthatóan egy kétdimenziós inverz DFT): 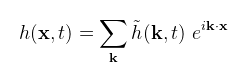
Ahol (előrevetítve, hogy egy displacement map-be lesz majd kiszámolva) 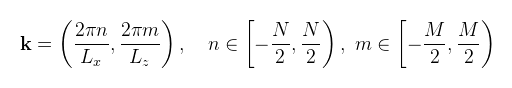
és N, M a displacement map felbontása, Lx, Lz pedig az óceándarakba térbeli méretei (méterben). A fenti kétdimenziós inverz DFT az x = (nLx/N, mLz/M) diszkrét pontokban adja meg a hullámok magasságát (ezt később ki fogom használni). (megj.: ezeket "lineáris" vagy "gravitációs" hullámoknak nevezik, de sekély vízben megjelennek "nemlineáris" hullámok is) A következő lépés egy analitikus hullám spektrum (jelölésben Ph(k)) kiválasztása, amiből a DFT együtthatói előállíthatóak. Két ilyen nevezetes spektrumot említek meg, az egyik a Pierson-Moskowitz spektrum, a másik a Phillips spektrum (erről nem találtam irodalmat), de mivel utóbbi az elterjedtebb, azt fogom használni. A képlete 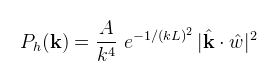
(megj.: HTML-ben nem tudok kalapot írni, itt normalizálást jelent) ahol L = V2 / g a legmagasabb hullám egy adott konstans V szélerősség mellett, w a szintén konstans szélirány, A pedig egy megválasztható konstans, amivel a hullámok magasságát lehet változtatni (általában egy kicsi érték). Tessendorf szerint a gyorsabb konvergencia érdekében célszerű az L-nél lényegesen kisebb (ε) hullámokat elhagyni, ami a képlet exp(-k2ε2)-tel való megszorzását jelenti (erre innentől módosított Phillips spektrumként hivatkozok). Az előbbi módosított Phillips spektrumot véletlenszerű értékekkel megszorozva, a Fourier együtthatókra (amplitúdókra) az alábbi képlet használható a t = 0 időpontban
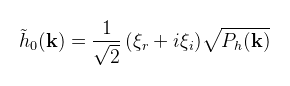
ahol ξr és ξi egy 0 várható értékű, 1 szórásnégyzetű normális eloszlásból húzott véletlenszerű értékek (ehhez lehet használni az std::normal_distribution osztályt, vagy a Box-Muller módszert). Ennek és a frekvenciáknak (ld. diszperziós reláció) a kiszámolását rátok bízom; csak le kell kódolni a képleteket (az eredményt pedig float textúrákba pakolni). Ha ezek megvannak, akkor a Fourier együtthatókat a következőképpen lehet kiszámolni valamilyen tetszőleges t időpontban: 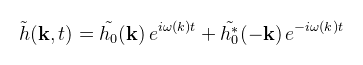
Mint később látni fogjuk, a kiinduló állapot szimmetriája miatt nem kell külön kiszámolni a negatív hullámvektorhoz tartozó együtthatókat. Erre a képletre innentől magasságspektrumként fogok hivatkozni. Ha elvégezzük rá az inverz DFT-t, akkor egy majdnem hihető óceánfelület-darabkát kapunk eredményül. A helyzet viszont az, hogy az óceánfelület nem csak a magasságában (heightfield) fluktuál, hanem az alapsíkjában is, ezáltal fodrozódásokat keltve (choppy field). Megfelelő magasságú hullám esetén ezek a fodrozódások egy hurkot állítanak elő a felületben, ettől ott az óceán habzani fog. Nézzük meg először a különbséget: 
A képeken pontosan ugyanabban az időpontban látható egy csak magasságban, illetve egy magasságban és alapsíkban is hullámzó felület. Utóbbi láthatóan "érdesebb", és jobban is emlékeztet az óceánra. Ennek eléréséhez az ún. Lie transzformáció 2D-s megoldását extrapolálja a dolgozat 3D-be. Az alapsíkbeli elmozdulás képletére így a következőt kapjuk: 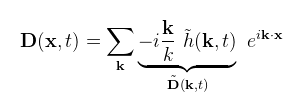
Ami szintén kétdimenziós inverz DFT, de szerencsére a Fourier együtthatói a magasságspektrumból kiszámolhatóak, ezáltal plusz két spektrumot kapva (gondolom mindenki látja, hogy vastag betűvel írtam, merthogy vektorértékű). A DFT linearitását kihasználva ez a két spektrum összevonható egybe. Mindegyik spektrumot (a kiindulásit is beleértve) kétdimenziós RG32F textúrákban tárolom, ami az ún. prefetch cache miatt hatékony compute shader implementációt tesz lehetővé. A kód kicsit hosszú, úgyhogy rövidíteni fogom: CODE
ivec2 loc1 = ivec2(gl_GlobalInvocationID.xy);
ivec2 loc2 = ivec2(N - loc1.x, M - loc1.y);
// kiindulási spektrum betöltése (amit előre kiszámoltatok)
vec2 h0_k = imageLoad(tilde_h0, loc1).rg;
vec2 h0_mk = imageLoad(tilde_h0, loc2).rg;
float w_k = imageLoad(frequencies, loc1).r;
// magasságspektrum
float cos_wt = cos(w_k * time);
float sin_wt = sin(w_k * time);
vec2 h_tk = ComplexMul(h0_k, vec2(cos_wt, sin_wt)) + ComplexMul(Conjugate(h0_mk), vec2(cos_wt, -sin_wt));
// "choppy" spektrumok (höfö: ez miért helyes?)
vec2 k = vec2(N / 2 - loc1.x, M / 2 - loc1.y);
vec2 nk = normalize(k);
vec2 Dt_x = vec2(h_tk.y * nk.x, -h_tk.x * nk.x);
vec2 iDt_z = vec2(h_tk.x * nk.y, h_tk.y * nk.y);
// eredmény kiírása
imageStore(tilde_h, loc1, vec4(h_tk, 0.0, 0.0));
imageStore(tilde_D, loc1, vec4(Dt_x + iDt_z, 0.0, 0.0));
Amint látható egy az egyben átírtam kódba a fenti képleteket; ennek fényében gondolom nem kell elmagyaráznom, hogy a kiindulási spektrumot hogyan kell kiszámolni. Annyit fűznék csak hozzá, hogy a hullámvektorokat megfordítottam; nem jöttem rá ugyanis, hogy az eredményül kapott óceán miért ellentétes irányba hullámzik, mint kellene (a legjobb tippem az, hogy az OpenGL fordított koordinátarendszerei miatt). A kód által előállított spektrumok (skálázás után) a következőképpen festenek: 
A sorrend ugyanaz, mint ahogy bemutattam; az első tehát a magasságspektrum, a másik kettő pedig az x és z-beli elmozdulás spektrumai (szétszedve). Mindegyiknél megfigyelhető az átlókra való szimmetria (ne tévesszen meg a spektrum alakja!), emiatt optimalizációs célból elég lenne csak az egyik felüket kiszámolni, de az megnehezítené a textúra címzést. (megj.: próbáljátok ki a kódmellékletben szétszedés nélkül; meg fogtok lepődni :) a matematikai magyarázata höfö) Végre elérkeztünk a cikk tetőpontjához, ami nem más, mint az imént kiszámolt spektrumok (kétdimenziós) inverz gyors Fourier transzformációja. Mielőtt ennek nekiállnánk, fejtsük ki a magasságmező inverz DFT-jét, hogy jobban lássuk mit is kell majd csinálni. Ehhez először is felteszem most már, hogy M = N, illetve Lx = Lz = N (itt használom ki az x korábbi felírását). Az előzőleg bemutatott FFT implementáció értelmében a hullámvektort is át kell előbb definiálni:
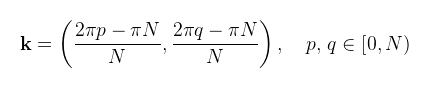
Mégegyszer azért, mert egyelőre nem térben akarom megkapni a hullámokat, hanem egy N×N-es textúrában (a spektrumokban van a valódi információ!). Ekkor kifejtve a magasságmező képletét (az olvashatóság miatt a fizikában megszokott jelölést használva) az alábbit kapjuk: 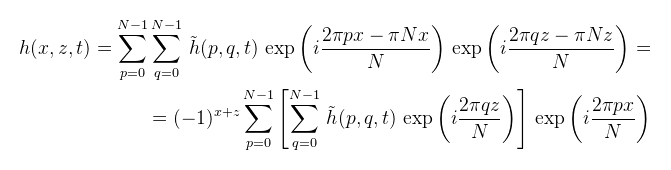
A kiemelések a már említett eiπ = -1 miatt tehetőek meg (ha nem hiszitek, ellenőrizzétek az Euler formulával), az átrendezések pedig az exponenciális függvény azonosságai miatt. A képletből egy különösen fontos dolog látszik: a kétdimenziós DFT szeparálható (ugyanúgy, mint pl. a Gauss szűrő). Elég tehát egydimenziós esetre megírni az inverz FFT algoritmust, majd lefuttatni először a spektrum soraira, utána pedig az oszlopaira. Lássuk akkor most már a teljesértékű compute shader-t: CODE
shared vec2 pingpong[2][N];
layout (local_size_x = N) in;
void main()
{
int z = int(gl_WorkGroupID.x);
int x = int(gl_LocalInvocationID.x);
// sor/oszlop betöltése az osztott memóriába
pingpong[1][x] = imageLoad(readbuff, ivec2(z, x)).rg;
barrier();
// a tömb átrendezése az FFT-hez
int nj = (bitfieldReverse(x) >> (32 - LOG2_N)) & (N - 1);
pingpong[0][nj] = pingpong[1][x];
barrier();
// pillangó szakaszok
int src = 0;
for (int s = 1; s <= LOG2_N; ++s) {
int m = 1 << s; // pillangó csoport magassága
int mh = m >> 1; // pillangó csoport magasságának fele
int k = (x * (N / m)) & (N - 1);
int i = (x & ~(m - 1)); // pillangó csoport kezdő sora
int j = (x & (mh - 1)); // pillangó index a csoportban
// WN-k twiddle factor
float theta = (TWO_PI * float(k)) / N;
vec2 W_N_k = vec2(cos(theta), sin(theta));
vec2 input1 = pingpong[src][i + j + mh];
vec2 input2 = pingpong[src][i + j];
src = 1 - src;
pingpong[src][x] = input2 + ComplexMul(W_N_k, input1);
barrier();
}
// eredmény kiírása
vec2 result = pingpong[src][x];
if (direction == 0) {
imageStore(writebuff, ivec2(x, z), vec4(result, 0.0, 1.0));
} else {
// a hullámvektor megváltoztatása miatt
float sign_correction = ((((z + x) & 1) == 1) ? -1.0 : 1.0);
imageStore(writebuff, ivec2(x, z), vec4(sign_correction * result, 0.0, 1.0));
}
}
Ravasz módon úgy írtam meg, hogy ne kelljen az indexeléssel bajlódni (viszont értelemszerűen kell egy textúra a köztes adatnak). A képletből kiemelt előjelet az érthetőség kedvéért ide raktam, de természetesen megspórolható az elágazás, ha nem itt végzem el, hanem a három hullámtextúra egyesítésekor (a kódmellékletben természetesen úgy szerepel). A workgroup shared memória méretkorláta miatt ez az algoritmus legfeljebb 1024×1024-es textúrákra működik, de ez annyira nem nagy baj, mert efölött már látható precíziós hibák jönnek elő. Ha esetleg nagyobb méretre van szükség, akkor globális memóriába pakolt bufferekkel az is megoldható, viszont értelemszerűen lassabb lesz. Na de lássuk az eredményt (mindhárom spektrumra): 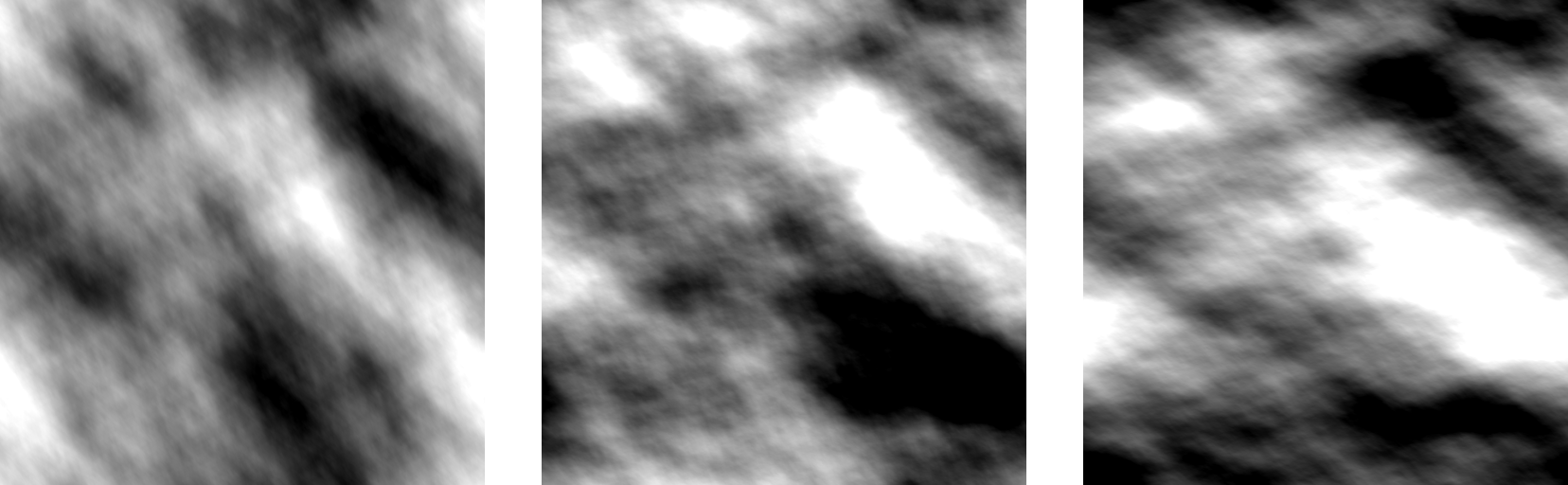
A képeken nem látszik, de higgyétek el, hogy mindegyik a neki megfelelő irányba mozog, illetve az amplitúdóknak megfelelően változik. Ezt a hármat összepakolva egy RGBA32F textúrába elő is áll a displacement map, amivel már lehet játszadozni. Ha eddig nem lett volna világos, a DFT miatt természetesen mindegyik periodikus. A hatékony de mégis látványos megvilágításhoz szükség van egy normal map-re, illetve az említett "habzáshoz" egy folding map kiszámolására (utóbbit az nVidia nem használja semmire, de majd megmutatom egy lehetséges alkalmazását).
CODE
ivec2 left = (loc - ivec2(1, 0)) & (N - 1);
ivec2 right = (loc + ivec2(1, 0)) & (N - 1);
ivec2 bottom = (loc - ivec2(0, 1)) & (N - 1);
ivec2 top = (loc + ivec2(0, 1)) & (N - 1);
vec3 disp_left = imageLoad(displacement, left).xyz;
vec3 disp_right = imageLoad(displacement, right).xyz;
vec3 disp_bottom = imageLoad(displacement, bottom).xyz;
vec3 disp_top = imageLoad(displacement, top).xyz;
vec2 gradient = vec2(disp_left.y - disp_right.y, disp_bottom.y - disp_top.y);
imageStore(gradients, loc, vec4(gradient, 2.0 * L / N, J));
Két okból nem használtam az említett GLSL függvényeket: egyrészt mert csak a fragment shader-ben érhetőek el, másrészt a kép széleinél helytelen eredményt adnak. Itt említem meg, hogy a % N és a & (N - 1) között az a lényeges különbség, hogy előbbi megtartja az előjelet, míg a másik átfordul (és egy periodikus textúra esetén nyilván ez a cél). A fodrozódás kiszámolásához hasonló dolgot kell tenni az ún. Jacobi mátrix formájában, ami szintén parciális deriváltakat tartalmaz, viszont vektorértékű függvényekre (és a fenti choppy field ilyen). A mátrix valamilyen x pontból az x + λD(x, t) pontba való transzformációt írja le, ahol λ egy megválasztható konstans, amivel növelni/csökkenteni lehet a kilengéseket (én fixen λ = 1.3-at használok): 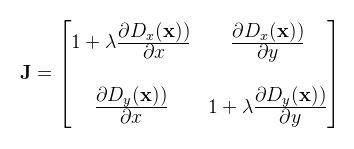
(megj.: a Cauchy-Riemann egyenletek miatt ez megegyezik az f = Dx + iDy függvény komplex deriváltjával) A mátrix determinánsa mondja meg a transzformáció egyediségét: amíg nem metszi önmagát (a hullám nem borult át magán), addig egyedi, invertálható, a determináns pedig pozitív értékű. Ennek kiszámolása szintén véges differenciákkal történik: CODE
vec2 dDx = (disp_right.xz - disp_left.xz) * (N / L);
vec2 dDy = (disp_top.xz - disp_bottom.xz) * (N / L);
float J = (1.0 + dDx.x) * (1.0 + dDy.y) - dDx.y * dDy.x;
Gondolom a 2×2-es mátrix determinánsának kiszámolására csak emlékeztek... Zárójelben, amikor a mátrix négyzetes, akkor az irodalmak egyszerűen csak Jacobian-nak nevezik (beleértve a determinánst is). 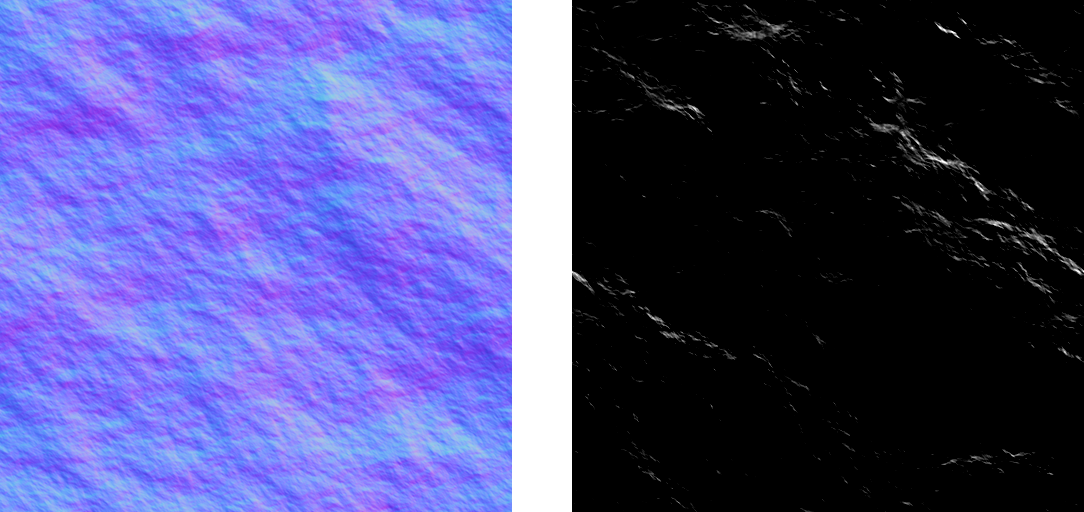
A gradienseket a szokásos normalize/mad függvényekkel alakítottam a megszokott formára, de ne felejtsük el, hogy az óceán (kvázi) sík felület, ami miatt nem kell tangent frame számolásokkal küzdeni. A folding map használatáról később írok. Most egy olyan rész jön, amit csak nagyvonalakban mutatok be, ugyanis ezt a kódot speciel egyszerűbb kimásolni, mint oldalakon keresztül magyarázni. Apró módosításokat végeztem csak rajta, például javítottam az indexelést, eltüntettem a degenerált háromszögeket, stb. Az egész egyébként az ún. geomipmapping elméleten alapul.

Ezen a képen persze látszik, hogy hol történnek a LOD szint váltások, de a generált kapcsolódási pontok miatt a konkrét óceánon egyáltalán nem vehetőek észre. Lehetne egyébként használni tessellation shader-t is, de sajnos a tesszellációs szint le van korlátozva 64-re, ami nekem nem volt elég (de az ARM/Mali mutat példát). Korábban lerögzítettem, hogy csak mély óceánnal foglalkozok, azzal is csak felülről (ha lemegyek alá, akkor megint egy BSDF modellt kellene alkalmazni). Ha valakit részletesen érdekel a sekély víz, illetve óceán alatti effektek, akkor javaslom a Crysis ingyenesen letölthető demóját, amiben az összes ezzel kapcsolatos HLSL shader megtalálható.
Ahol ρs a BRDF lufi "hosszát" jelenti, αx és αy az x illetve y iránybeli "vastagságát", h pedig a normalizálatlan félvektor. A teljes shader kód az alábbi módon fest, de a Ward modellhez saját kútfőből számoltam ki az értékeket; nem kerestem referenciát: CODE
vec4 grad = texture(gradients, tex);
vec3 n = normalize(grad.xzy);
vec3 v = normalize(vdir);
vec3 l = reflect(-v, n);
// Fresnel faktor (levegő IOR: 1.000293f, víz IOR: 1.33f)
float F0 = 0.020018673;
float F = F0 + (1.0 - F0) * pow(1.0 - dot(n, l), 5.0);
// tükröződő égbolt
vec3 refl = texture(envmap, l).rgb;
// habzás (az ARM/Mali példakódja alapján)
float turbulence = max(1.6 - grad.w, 0.0);
float color_mod = 1.0 + 3.0 * smoothstep(1.2, 1.8, turbulence);
// napfény (Ward modell)
const vec3 sundir = vec3(0.603, 0.240, -0.761);
const float rho = 0.3;
const float ax = 0.25;
const float ay = 0.1;
vec3 h = sundir + v;
vec3 x = cross(sundir, n);
vec3 y = cross(x, n);
float mult = (ONE_OVER_4PI * rho / (ax * ay * sqrt(max(1e-5, dot(sundir, n) * dot(v, n)))));
float hdotx = dot(h, x) / ax;
float hdoty = dot(h, y) / ay;
float hdotn = dot(h, n);
float spec = mult * exp(-((hdotx * hdotx) + (hdoty * hdoty)) / (hdotn * hdotn));
my_FragColor0 = vec4(mix(oceanColor, refl * color_mod, F) + sunColor * spec, 1.0);
Az értékek változtatásával lehet erősíteni, szűkíteni, nyújtani a tükrözött fényt. Annyit elmondanék, hogy a demóban nem HDR-ben rajzolok (nem találtam megfelelő égboltot), a Ward modell 1-hez való integrálását pedig nem ellenőriztem, amitől lehet, hogy egy kicsit "erős" (ezen a paraméterek buherálásával lehet segíteni). A szélességét szintén empirikusan határoztam meg, hogy az égbolthoz nagyjából igazodjon (de a valóságban ennél jóval keskenyebb). 
Nyilván egy teljesértékű óceánhoz ez nem elég. A Ross modellhez itt található egy mindent részletező cikk, amiket én nem csináltam meg (például sík tükröződéseket). Ha valaki késztetést érez rá, akkor javaslom, hogy screen space reflection módszerrel próbálkozzon. Utolsó erőfeszítésként az nVidia javaslatai alapján tüntessük el a periodicitásból adódó (és igen zavaró) ismétlődéseket. Az ötlet annyi, hogy egy bizonyos távolságtól kezdve cseréljük le az FFT alapú óceánt egy Perlin zaj alapú hullámra, ami érdekes módon még ismételve sem produkál látható artifact-okat (így például használják domborzat, felhő, stb. megjelenítéséhez is). A képlete leegyszerűsítve (saját formalizáció):
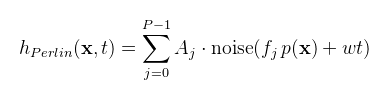
Ahol P az oktávok száma, Aj és fj a j-edik oktáv amplitúdója illetve frekvenciája, p(x) a vetített textúra koordináta, noise pedig az alap Perlin textúra. A hullám, illetve a normálvektorai közvetlenül generálhatóak shader-ben: CODE
#define BLEND_START 8 // m
#define BLEND_END 200 // m
const vec3 perlinFrequency = vec3(1.12, 0.59, 0.23);
const vec3 perlinAmplitude = vec3(0.35, 0.42, 0.57);
const vec3 perlinGradient = vec3(0.014, 0.016, 0.022);
float dist = length(vdir.xz);
float factor = clamp((BLEND_END - dist) / (BLEND_END - BLEND_START), 0.0, 1.0);
CODE
// displacement (vertex shader)
if (factor < 1.0) {
float p0 = texture(noise, ptex * perlinFrequency.x + wind_dir * time).a;
float p1 = texture(noise, ptex * perlinFrequency.y + wind_dir * time).a;
float p2 = texture(noise, ptex * perlinFrequency.z + wind_dir * time).a;
perl = dot(vec3(p0, p1, p2), perlinAmplitude);
}
disp = mix(vec3(0.0, perl, 0.0), disp, factor);
CODE
// gradiens (fragment shader)
if (factor < 1.0) {
vec2 p0 = texture(noise, ptex * perlinFrequency.x + wind_dir * time).rg;
vec2 p1 = texture(noise, ptex * perlinFrequency.y + wind_dir * time).rg;
vec2 p2 = texture(noise, ptex * perlinFrequency.z + wind_dir * time).rg;
perl = (p0 * perlinGradient.x + p1 * perlinGradient.y + p2 * perlinGradient.z);
}
grad.xy = mix(perl, grad.xy, factor);
color_mod = mix(1.0, color_mod, factor);
A többi pedig ugyanaz, mint eddig. Összehasonlító kép: 
A módszer akkor is működik, ha elég magasról nézek közvetlenül az óceánfelületre, ekkor viszont a kép közepén lesz részletes és a szélei felé vált át Perlin hullámokba.
Az ehhez hasonló mély matematikai cikkeknél általánosan jellemző, hogy az implementáció gyorsan megvan, az elméleti háttér szöveggé formálása viszont rengeteg időt elvisz. Adódik ez például abból, hogy egy adott matematikai fogalom felvezetése után bennem is felmerülnek kérdések, hogy "na de miért van ez így?". A válasz felkutatása során pedig még mélyebbre ásom magam a már egyébként is nehéz elméletekben.
(megj.: bal oldal: Ward modell, jobb oldal: Blinn-Phong modell; előbbi a valóságnak megfelelve elér teljesen az óceán végéig) Addig is a kódmelléklet elérhető a szokott helyen, a teljes mértékig felturbózott óceánról készült videó pedig itt tekinthető meg (állítsátok át 1080p-re, ha nem abban indul). A diagramok gnuplot kódját kérésre odaadom. Höfö:
Irodalomjegyzék http://evasion.imag.fr/.../Jonathan/articlesCG/waterslides2001.pdf - Simulating Ocean Surfaces (Jerry Tessendorf, 2001) https://people.cs.clemson.edu/~jtessen/papers_files/coursenotes2004.pdf - Simulating Ocean Water (Jerry Tessendorf, 2004) https://pdfs.semanticscholar.org/330e/... - Notes on the Ward BRDF (Bruce Walter, 2005) http://www-evasion.imag.fr/~Fabrice.Neyret/.../NV_OceanCS_Slides.pdf - Ocean Surface Simulation (nVidia) https://hal.inria.fr/inria-00443630/file/article-1.pdf - Real-time Realistic Ocean Lighting [...] to BRDF (EUROGRAPHICS, 2010) https://dspace5.zcu.cz/bitstream/11025/11943/1/Tian.pdf - Ocean wave simulation by the mix of FFT and Perlin (WSCG, 2014) https://.../Realtime_GPU_ocean_rendering.pdf?dl=0 - Real-time GPU-driven Ocean Rendering on Mobile (ARM/Mali, 2015) http://developer.download.nvidia.com/... - Ocean simulation and rendering in War Thunder (nVidia, 2015) https://tubdok.tub.tuhh.de/... - Realtime GPGPU FFT Ocean Water Simulation (Hamburg University of Technology, 2017) http://mogi.bme.hu/TAMOP/mereselmelet/ - Méréselmélet (BME, 2014) |


