A 21. század technológiai vívmányainak egyik jeles képviselőjén (melyet hívjunk most shader-nek) vérszemet kapva felmerült az igény arra, hogy a GPU-t ne csak rózsaszín pónilósimogató játékokra használják, hanem tudományos berkekben régóta problémát jelentő algoritmusokat is átvigyenek oda. Ami annyira nem is volt egyszerű, hiszen 2001 környékéről beszélünk, amikor még épphogy assemblyben lehetett shadereket írni, sőt a probléma megoldását egy más szemlélettel át kellett alakítani az akkori API-k számára emészthető formába (pont, vonal, háromszög).

Egy elterjedt megoldás volt (egy unalmasabb adatbáziskezelés gyakon tűnt fel) PlayStation 3-ak összekötése hálózaton keresztül, amiken aztán valamilyen matematikai algoritmust futtattak (az ELTE amúgyis nevezetes a prím- és ikerprím keresési eredményeiről). A GPU ilyen jellegű felhasználása GPGPU néven terjedt el (General Purpose processing on GPUs).

A cikket eredetileg OpenCL-ről kellett volna írnom (Open Compute Library), de több okból is elvetettem ezt az ötletet:

• külön fel kell telepíteni
• a munkahelyi nVidia kártyámon nem hajlandó működni
• a driver támogatás elképesztően rossz
• az OpenGL-el való interakció is borzasztó: megakasztja a pipelinet (glFinish)
• fapadosabb mint az OpenGL

Egyetlen előnyét azért ki lehet még emelni: CPU-n is képes működni, tehát az előbb említett matematikai problémákra még mindig elég jól használható...lenne, csak az a gond, hogy arra CUDA-t használnak inkább (az nVidia komolyan veszi a driver írást). Pongyolán azt lehet mondani, hogy az OpenCL nem grafikai jellegű GPU programokhoz használható, amíg nem befolyásolja a driver minősége (pl. mert csak egy gépen futtatod).

A valódi cél viszont a GPGPU grafikában való felhasználása, ezért úgy döntöttem, hogy a lehető legújabb technológiáról írok cikket, ami a compute shader. A nevéből is kitalálható, hogy ez szorosan része a választott API-nak (jelen esetben OpenGL 4.3), így ilyen célra sokkal hatékonyabb. A másik oldalon DirectX 11-től érhető el (de korlátozottan DX10-es kártyán is fut).

Zárójelben még annyit említenék meg, hogy így 2013 után valami bábeli zűrzavar kezd kialakulni a grafikai API-k körül, ugyanis sorra jelennek meg új, nagyrészt platformfüggő API-k (holott az igény pont az lenne, hogy csak egy legyen, de mindenhol). Néhány ezek közül: Mantle (AMD), DirectX 12 (Microsoft), Metal (Apple), OpenGL 5 (Khronos alkoholterápiás csoport). A közös ezekben az, hogy (egymásról másolva) egy sokkal hardverközelibb "élményt" nyújtanak, ami elég meglepő tekintve, hogy programozás területén eddig az absztrakció volt a menő (nesze neked ELTE bevprog...). Mindenesetre mindegyikben alapból benne van a compute shader valamilyen formában, ez tehát plusz egy indok arra, hogy foglalkozzak vele.

A GPU egy massively parallel architektúra, azaz a teljesítményét brutális párhuzamosítással éri el. A CPU és GPU közti különbséget legjobban ez a videó szemlélteti: míg a CPU néhány magja szekvenciális feldolgozásra van optimalizálva, addig a GPU a több ezer magjával a (masszívan) párhuzamos feldolgozásra épít.

A terminológiákban elég sok kavarodás van, hogy hogyan épül fel egy GPU. Fentről megközelítve egy Kepler architektúrájú nVidia GPU valahány darab streaming multiprocessor-t tartalmaz (SMX), egy ilyen SMX-nek van 192 magja (CUDA core). Egy core aztán még tovább bomlik egyéb egységekre (integer és float ALU, stb.). Én itt és most compute unit alatt SMX-et értek (vigyázat, a Khronos group alkoholistái core-nak hívják). Azért veszélyes elnevezés ez, mert architektúránként változhat, hogy mi felel meg egy compute unit-nak.

Egy konkrét példán keresztül a Tesla architektúrájú GeForce GTS 250-nek 16 compute unit-ja van, de összesen 128 core állítható munkába (tehát mondhatjuk, hogy compute unit-onként 8 mag). Ez ma már egy alsó kategóriás kártya, a mostani legújabb nVidia kártyának (GeForce GTX Titan) 2688 core-ja van, viszont Kepler architektúra (tehát akkor 14 compute unit-ot kéne mondani rá, ami furcsán hangzik a 16-al szemben). Az itt leírt algoritmusokat egy GeForce GTX 650-en implementáltam (384 core, Kepler).

A GPGPU központi fogalma a kernel, ez maga a program, ami több száz példányban fog párhuzamosan futni. Az elnevezés onnan jön, hogy szemléletben megfelel egy klasszikus for ciklus magjának. A végrehajtási modellt úgy kell elképzelni, hogy először is veszünk egy problémateret (1, 2 vagy 3 dimenziósat). A végrehajtás az N×M×L-es problématéren (global workspace) történik, N×M×L darab work item által. Egy ilyen work item megfelel egy CUDA thread-en futó kernelnek. A work item-ek össze vannak csoportosítva work group-okba (CUDA thread block vagy local workspace). Az alábbi ábra a 2D esetet szemlélteti:

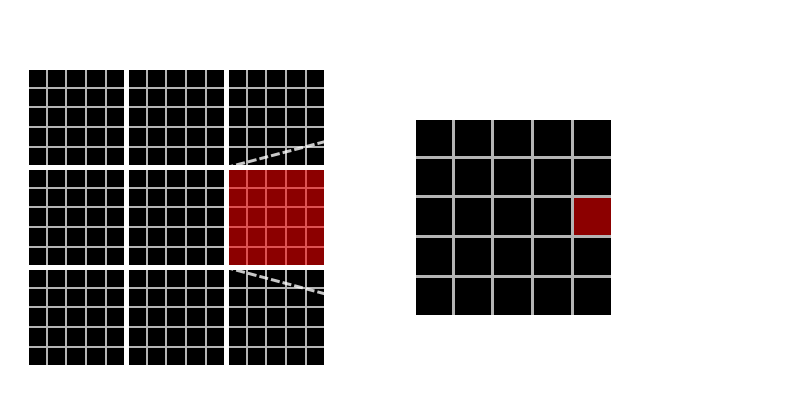
Egy compute unit több work group-ot is futtathat egyszerre, de egy work group-on belül egyszerre 32 thread fut egymás mellett (ez megint csak nVidia kártyákra igaz, AMD-n úgy tudom 64). Az egy compute unit-on való futás miatt az egy work group-on belüli work item-eknek van közös memóriája, melyet szinkronizációs utasításokkal lehet írni/olvasni. Természetesen globális memória is van, de azok már csak bufferként jelennek meg.

Amit fontos még megemlíteni, hogy egy kernel milyen memóriákat tud használni:

• private: a work item (thread) lokális memóriája, pl. kernelen belül dekarált változóknak
• shared: a work group-on belüli közös memória (kernelen kívül deklarált változók)
• global: minden work item számára látható memória (bufferek, image-ek)
• texture: cache-elt memória textúráknak
• constant: csak olvasható memória (uniformok)

A globális memóriában levő adat alignolt kell legyen a méretéhez (cím = k ⋅ méret), amennyiben hatékonyan akarsz írni/olvasni belőle. CUDA-ban és OpenCL-ben ez viszonylag széles skálán mozog (van 1 bájtos típus is), GLSL-ben viszont tipikusan 16 bájttal működik jól. A teszteléshez használt Radeon 6750M ígyisúgyis kipaddelte 16 bájtra, ami egyébként nem lenne nagy baj, csak mellette még nem is működik a program (driver hiba).

A bevezetés után rátérnék arra, hogy OpenGL 4.3-ban hogyan mutatkozik meg ez a compute shaderes buli. Négy új extension van ami ehhez szorosan kapcsolódik:

• ARB_compute_shader: lehetővé teszi compute shaderek használatát
• ARB_shader_image_load_store: a shader tudja írni/olvasni a textúrákat, mint image objektum
• ARB_shader_storage_buffer_object: nagyméretű bufferek, tetszőleges formátumú adattal
• ARB_shader_atomic_counters: globális számláló (ez régebb óta van)

Ezekhez tartozik egy rakás új OpenGL hívás is, azokra majd később lesz példa. Itt most egy mezei compute shadert firkálok csak ide, ami sakktáblamintát rajzol egy textúrába:

CODE // SHADER oldal #version 430 layout(binding = 0) uniform writeonly image2D img; // egy workgroup 16x16-os layout(local_size_x = 16, local_size_y = 16) in; void main() { ivec2 loc = ivec2(gl_GlobalInvocationID.xy); vec4 color = vec4(0.0, 0.0, 0.0, 1.0); if( (loc.x / 16 + loc.y / 16) % 2 == 1 ) { color.r = sin(time) * 0.5 + 0.5; color.g = cos(time) * 0.5 + 0.5; color.b = sin(time) * cos(time) * 0.5 + 0.5; } imageStore(img, loc, color); }

CODE // OPENGL oldal GLuint texture = ...; GLuint computeprog = ...; GLint time_loc, img_loc; // berakja a textúrát a 0-s binding point-ba glBindImageTexture( 0, texture, 0, GL_TRUE, 0, GL_WRITE_ONLY, GL_RGBA8); glUseProgram(computeprog); time_loc = glGetUniformLocation(computeprog, "time"); img_loc = glGetUniformLocation(computeprog, "img"); glUniform1f(time_loc, time); glUniform1i(img_loc, 0); // compute shader futtatása (8x8 darab workgroup) glDispatchCompute(8, 8, 1);

Az első szembetűnő dolog a sok layout minősítő. Ezek többnyire hint-ek a drivernek (pl. sampler esetében megmondható a textúra formátuma). Végre meg lehet adni binding point-ot is (a.k.a. regiszter), így nem kell uniformként beállítani.

A textúra létrehozását gondolom nem kell bemutatni, de látható hogy 128x128-as. A shadert is teljesen hasonlóan kell betölteni mint eddig, csak a glCreateShader(GL_COMPUTE_SHADER) hívásban különbözik a régitől. A programhoz csak ezt a compute shadert kell hozzáattacholni (és nem is lehet mást).

A sakktábla mintában egy csempe egy workgroup. Azt, hogy éppen melyik csempében vagyok ki lehet számolni a beépített gl_GlobalInvocationID változóból. Minden második csempe színes lesz, a többi fekete. Megjegyezném, hogy valójában elég lenne workgrouponként egyszer kiszámolni, hiszen az első 32-es thread csoport lefutása után már pazarlás (később).

A következő bekezdésekben példákon keresztül mutatom be részletesebben a használatot és a megvalósítható technikákat. Erősen ajánlott az OpenGL 4.4 és GLSL 4.3 specifikáció tanulmányozása, ugyanis minden ide vonatkozó dolog le van benne írva (még ha nehéz is megtalálni).

Ebbe a kategóriába tartozik minden olyan (megvilágítási) módszer ami a képernyőt csempékre osztva optimalizálja a fragmentekre ható fények számát. Még a compute shader előtti időkben a deferred lighting legnagyobb előnye az volt, hogy sok fényforrást tudott kezelni, így játék szempontból az lett a meghatározó (és a forward rendering háttérbe szorult).

A tile alapú forward+ rendering motivációja az, hogy a forward rendering előnyeit megtartva (MSAA) rengeteg fényforrást lehessen használni. Bár így visszatérhetne régi nagy fényéhez, ugyanezt a módszert lehet alkalmazni deferred lightinghoz is, így a nagy visszatérés egyelőre elmaradt. Tile alapú deferred renderer például a Frostbite 2 engine, forward+ alapú pedig az AMD Leo demo-ja.

A cikkhez én egy forward+ renderert implementáltam le, mert ahhoz van kevesebb anyag. Emlékeztetőül a klasszikus forward rendering pszeudokódja:

A forward+ annyiban javít ezen, hogy a fényekre vonatkozó (belső) ciklust átviszi shaderbe. Most mindenki akadékoskodik, hogy "dehát ezt eddig is meg lehetett volna csinálni". Persze, csak épp objektumonként mondjuk 1000 fényre ciklust futtatni shaderben elég gáz (hacsak nem diavetítés a cél). Az észrevétel az, hogy normális programozók esetében a sok fényforrás kvázi egyenletesen oszlik el a képernyőn, tehát az egy pixelre ható fények száma nagyságrendekkel kisebb, mint az összes fény száma.

Tehát ha a képernyőt részekre osztom és mindegyik részre meg tudom mondani, hogy milyen fények hatnak oda, akkor hatalmas teljesítményjavulást lehet elérni. Először leírnám a renderer és a compute shader lépéseit (a Kibaszott Fontos Lépés ^®-eket KFL-nek rövidítem):

• z-only pass (KFL): alapkövetelmény, hogy 0 overdraw legyen a későbbiekben!
• compute shader: egy workgroup 16x16-os (az egy tile)
  • lineáris min/max z érték kiszámolása a tile-on belül
  • a tile-hoz tartozó frustum meghatározása
  • a fényeket szétosztva a work itemek között, frustum culling
  • a tile-ban levő fényeket eltárolni egy láncolt listában
• depth write disable (KFL): a driver általában már ebből is ki tudja találni, hogy early z-test kell
• minden objektumra:
  • kirajzolás az akkumuláló shaderrel (fragmentenként végigmegy a megfelelő láncolt listán)
• gamma korrekció (KFL): több fényforrást enélkül meg se próbálj

A feladat megcsinálni ezt compute shaderben, beleértve a láncolt listában való tárolást is. Aki tudja mi az az uniform buffer, annak ismerős lesz a shader storage buffer (SSBO) is, merthogy teljesen hasonló, csak sokkal nagyobb lehet (legalább 16 MB-ig támogatnia kell a drivernek), illetve írható shaderből. DirectX 11-ben egy UAV-al ellátott buffer felel meg ennek (unordered access view). A programban a következő bufferek vannak használva:

• lightbuffer (SSBO): ez tárolja a fényeket
• headbuffer (SSBO): a láncolt listák fejelemei (tile-onként egy)
• nodebuffer (SSBO): a láncolt listák elemei (elég nagy a szélsőséges esetek kezeléséhez is)
• nextInsertionPoint (AC): atomic counter , hogy tudjuk hová lehet beszúrni a nodebuffer-ben
• depthSampler (SAMPLER): depth textúrát nem lehet image-ként lepasszolni (nem tudom miért)

Az SSBO-k és az AC létrehozása és feltöltése ugyanúgy történik, mint az eddigi bufferek esetében, értelemszerűen a hozzá tartozó flaget megadva a glBindBuffer-nek. Annyit mondanék, hogy foglaláskor érdemes csak glBufferData-t hívni, minden más íráskor már glMapBuffer-t. Ha ugyanis a shared memóriába pakolja a driver (pl. a fényeket tartalmazó buffer ilyen), akkor visszaad egy direkt pointert abba a memóriába.

A használat viszont már egész más mint a "régi" bufferek esetében. GLSL oldalon a buffert egy interface block definiálja, a megfelelő minősítőkkel. Egy ilyen blokk tartalmazhat indefinit tömböt is (ez kb. megfelel egy pointernek):

CODE // SHADER oldal #version 430 struct ListHead { uvec4 StartAndCount; }; layout(std140, binding = 0) writeonly buffer HeadBuffer { ListHead data[]; } headbuffer; // ... nodebuffer (1), lightbuffer (2) layout(binding = 0) uniform atomic_uint nextInsertionPoint; layout(binding = 0) uniform sampler2D depthSampler; // ... folyt ...

CODE // OPENGL oldal glBindBufferBase(GL_SHADER_STORAGE_BUFFER, 0, headbuffer); glBindBufferBase(GL_SHADER_STORAGE_BUFFER, 1, nodebuffer); glBindBufferBase(GL_SHADER_STORAGE_BUFFER, 2, lightbuffer); // inicializálja az atomic countert glBindBuffer(GL_ATOMIC_COUNTER_BUFFER, counterbuffer); GLuint* counter = (GLuint*)glMapBuffer( GL_ATOMIC_COUNTER_BUFFER, GL_WRITE_ONLY); *counter = 0; glUnmapBuffer(GL_ATOMIC_COUNTER_BUFFER); glBindBufferBase(GL_ATOMIC_COUNTER_BUFFER, 0, ...); glBindTexture(GL_TEXTURE_2D, depth_tex); // compute shader futtatása glUseProgram(...); glDispatchCompute(workgroupsx, workgroupsy, 1);

Kezdeném azzal, hogy mi az az std140. Ez egy platformfüggetlen memory layout, amelyet a szabvány definiál (OpenGL spec 7.6.2.2): a struktúra tagjai alignolva lesznek a megadott szabályok szerint. Az std430 teljesen hasonló, viszont nem paddeli ki 16 bájtra az egyébként érvényes struktúrákat (pl. uvec2).

Van egy másik ilyen layout (packed) ami arra szolgálna, hogy ne történjen paddelés, de az is csak nVidia kártyákon megy (mily meglepő) és egyébként platformfüggő, szóval ne használjátok. Én annyira óvatos vagyok ezzel, hogy a vec3 + float kombót se vállalom be, mert szerintem az AMD 32 bájtra paddelné ki... Az offseteket egyébként le lehet kérdezni OpenGL oldalon a glGetActiveUniform hívással (én ezt eddig nem tettem meg).

Csak a szemléltetés kedvéért megmutatom hogyan lehet shared változókat használni a compute shaderben. Például egy adott tile-ra vonatkozó mélység ilyen shared változó:


A lényeg a barrier() hívás, ami addig blokkol amíg a work group-on belül minden thread el nem jutott arra a pontra. Ennek tudatában már világos a működés: minden thread atomi utasításokkal buherálja a két shared változót, majd amikor mindegyik elért a barrier-hez, a változókban ott van a helyes érték. Annyi szépséghiba van, hogy ezek az atomi utasítások csak int és uint-re működnek.

A továbbiakban igazából olyan izgalmas dolgok nincsenek már. A frustum-okat nagyon könnyen meg lehet határozni, hiszen a síkegyenletről tudjuk, hogy kovariáns vektor, azaz:

P⋅v = 0    ⇔    P⋅M^-1M⋅v = 0    ⇔    P⋅MM^-1⋅v = 0
Tehát ha egy síkegyenletet screen spaceből vissza akarok transzformálni world space-be, akkor mindössze jobbról kell szorozni a viewproj mátrixxal. Most egyesek pánikba esnek, hogy na de a perspective division biztos bekavar... Nem kavar be, ha most kifejtjük a síkegyenletet clip space-ben, akkor:

(a, b, c, d) ⋅ (wx, wy, wz, w)^T = (wa, wb, wc, wd) ⋅ (x, y, z, 1)^T
Tehát ha a viewproj-al való transzformáció után normalizálod a síkegyenletet, akkor tökéletesen működni fog. Ja és screen spaceben mik a síkegyenletek? Annyit segítek, hogy a teljes projekciós mátrixra a screen space-beli frustum egy [-1, 1]³ kocka. Azt felosztod a tile-oknak megfelelően (tipp: csak a d komponensben különböznek) és kiszámolod a síkokat.

A végén még a láncolt listába való írkálásról kéne mondani valamit. A listát hátulról építem fel az alábbi módon:


A TileLightStart tehát arra szolgál, hogy tudjam melyik volt az előző listaelem helye (csak a helye kell), hiszen a következőnek beszúrt elem erre kell mutasson. A TileLightCount-ra valójában nincs szükség, de ha már úgyis ki van paddelve a struktúra, akkor legyen ott (debug célra).

Az akkumuláló fragment shadert gondolom már nem kell bemutatni. Kiolvassa az SSBO-kból amit kell, és elvégzi a megvilágítást. Az aktuális tile meghatározható a gl_FragCoord-ból.

A teljesítményről annyit, hogy a felbontástól és az egy tile-ra ható fények számától függ. Az utóbbihoz nyilván kapcsolódik a fények száma, sugara és a tile-ok mérete, de alapvetően nem a compute shader a lassú, hanem a fények rajzolása.

Ehhez speciel nem kell compute shader, SSBO viszont ajánlott. Az előzőhöz képest ez sokkal egyszerűbb algoritmus, mert csak beleírja a láncolt listába a fragmenteket (mélységgel együtt), viszont egy bruteforce megoldásnak tekintendő. A klasszikus AMD implementációhoz képest tettem néhány eltérést, ugyanis:

• alapesetben brutálisan sok memória (attól függ hány átlátszósági réteget akarsz megengedni)
• az előző algoritmushoz képest a buffer bármikor betelítődhet
• a rétegek lekorlátozása esetén nagyon nem mindegy mit írsz a láncolt listába

Az (eredeti) algoritmus lényege pont a fordítottja a fenti forward+ renderernek: az átlátszó objektumokat egy speciális vertex + fragment shaderrel rajzolja ki, ami a rendertargetbe még nem ír semmit, hanem helyette láncolt listába pakolja őket (képernyőpontonként egy lista). A láncolt listákat aztán egy fullscreen fragment shaderben rendezi és elvégzi a blendelést.

A láncolt listás bufferek teljesen hasonlóak mint fent, tehát van egy headbuffer (4 bájt per pixel elég) és egy nodebuffer (16 bájt per pixel elég). Na igen, de ha mondjuk 4 rétegig akarsz rendezni és a képernyőd 1920×1080-as (1080p, fullHD), akkor egy gyors fejszámolással az 126 MB (+8 MB a fejelemeknek). Ha a packed layout működne, akkor 95 MB (+4 MB)-ra letolható, de csak nVidia kártyákon működik rendesen (höfö dörömbölni az AMD-nél, hogy tanuljanak meg drivert írni). Az std430-at nem próbáltam, az egy picit javíthat (fejelemek).

Egy további probléma, hogy sok "fölösleges" fragment is kikerül, hiszen az objektum rajzolásakor alapesetben nem látható részek is beleíródnak a bufferbe (melyeket az önmagával való z-test kiszórt volna egyébként). Az implementációmban jelenleg jelen van egy elég ronda z-fight szerű dolog, amit még nem tudtam kiküszöbölni, de lehet hogy ez okozza. Persze meg lehetne oldani egy kézi z test-el, de akkor meg az objektum saját részei nem látszanak át rajta, és a módszer nagyrészt értelmét veszti... (legalábbis a költségének fényében).

Az eredeti algoritmushoz képest a következő dolgokban térek el:

• listánként 4 elemnek foglalok le helyet
• a rendezést a kigyűjtő fragment shaderbe vittem át
• csak a 4 legközelebbi fragmentet engedem be (a listát frissíteni kell)

Az így megvalósított rendezés sok adatmozgatással jár (a láncolt listából nem dobhatok ki elemet, mert nem tudom resetelni az atomic countert), így teljesítményben esetleg rosszabb, viszont a képernyő minden pixele kap lehetőséget. Rendezéshez a beszúró rendezés a legcélszerűbb, mert rendezett listára lineáris.


Most furcsának tűnik, hogy miért másolom ki a lista elemeit, de így sokkal tisztább és érthetőbb a kód. A helyes működéshez a fejelemlistát inicializálni kell glClearBufferData-val vagy shaderrel (speciel az előbbi jobban hangzik). Helytakarékosságból a fragment színét be lehet tömöríteni uint-be a packUnorm4x8 függvénnyel.

Ami egy sokkal lényegesebb dolog, az maga az alpha blending. Nézzük először mi történne normál esetben:

  final_color = mix( ... mix(mix(bg, c₁, a₁), c₂, a₂) ..., c_n, a_n);
  final_color = ( ... (bg * (1 - a₁) + c₁ * a₁) * (1 - a₂) + c₂ * a₂) * ... * (1 - a_n) + c_n * a_n

Ha most ezt kifejtem, akkor:

  final_color = bg(1 - a₁)(1 - a₂)...(1 - a_n) + c₁a₁(1 - a₂)...(1 - a_n) + ... + c_na_n

Legyen:

  accum_alpha = (1 - a₁)(1 - a₂)...(1 - a_n)
  accum_color = c₁a₁(1 - a₂)...(1 - a_n) + ... + c_na_n

Ezt adja ki az akkumuláló fragment shader és ekkor final_color = bg * accum_alpha + accum_color, ami megfelel annak, hogy glBlendFunc(GL_ONE, GL_SRC_ALPHA)-t hívsz. A fragment shader kódja innen már kitalálható.

A memóriahasználathoz annyit tudok hozzáfűzni, hogy lehet több lépésben is csinálni ezt a dolgot (pl. felosztani a képernyőt 4 csempére), de annak tejesítménybeli ára van, hiszen annyiszor kell leküldeni a geometriát. Egy rosszabb hír, hogy játékokban sok esetben közel sem elég 4 réteg. Szóval az okosabb módszerek még mindig menőbbek, lényeges látványbeli különbség nélkül.

Ez megint egy olyan dolog amihez nem feltétlenül kell compute shader, hiszen van tessellation shader is, ami limitáltabban, de tudja ezt. Anyagot viszont nem találtam hozzá, úgyhogy compute shaderrel csináltam meg. A rend kedvéért idefirkálom a NURBS görbe definícióját: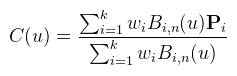

Ahol a P_i-k a kontrollpontok (k darab), n a görbe foka (k > n), a B_i,n-el jelölt bázisfüggvények pedig rekurzívan vannak megadva: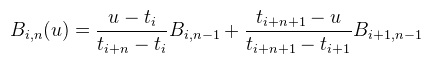


És a nulladfokú bázisfüggvény, ami a legtöbb problémát okozza: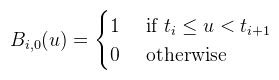


Ahol t₁ ≤ ... ≤ t_{k + n + 1} az úgynevezett knot vektor, például { 0, 0, 0.1, 0.4, 0.4, 1 }. A nulladfokú bázisfüggvény tehát két megfelelő knot között (knot span) 1 máshol 0, egy n-edfokú pedig a hozzá tartozó n + 1 spanon nemnulla.

Egy kicsit a görbe természetéről: egy adott pontra legfeljebb n + 1 kontrollpont hathat (ez később hasznos lesz). Hogy melyek, azt a knot vektor mondja meg. Tehát ahogy a paraméter (u) halad végig a knot spanokon, újabb kontrollpontok aktiválódnak, a régiek meg deaktiválódnak. Ha egy knot többször megjelenik (multiplicitás), az a görbe folytonos diffhatóságát csökkenti. Ha egy knot multiplicitása n + 1, akkor a hozzá tartozó egyetlen kontrollpontban a görbe nem diffható többé (C⁰ folytonos).

Na de miért rossz ez a definíció? Például azért, mert egyik irodalom se írja le, hogy u honnan a fenéből van. Jajj dehát biztos a [0, 1] intervallumból... hát nem. Meg azért is, mert a bázisfüggvényekben simán oszthat 0-val, és azt 0-nak kell tekinteni, különben nem működik.

Ha most ránézünk a görbe képletére akkor ott van a nevezőben egy normalizációs faktor (NF), amiről pongyola módon azt gondolná az ember, hogy sosem lehet nulla (hacsak minden súly nulla), sőt a legtöbb irodalom figyelembe se veszi, hogy nulla lehet. A nagyobbik probléma, hogy nemnulla értékek esetén is el tudja rontani a görbét (a folyt. diffhatóságát "véletlenül" lecsökkenti).

A bázisfüggvényeknek van egy olyan tulajdonsága, hogy adott u-ra az összegük 1 (partition of unity, egységosztás), és ezt a baromságot minden irodalom el is fogadja, mert egyik se csinálta meg soha. Nem, baromira nem mindig 1 az összegük, és ezzel meg is csinálom az első javítást a definíción:

Javítás 1: a görbe csak olyan u-kban van értelmezve, ahol az egységosztás tulajdonság teljesül.
Persze, akkor mondani kell egy olyan esetet, amikor nem teljesül: bármely olyan knot vektor, amelyikben az első vagy utolsó knot multiplicitása (m) nem n + 1. Általánosan a következő mondható (multiplicitástól függetlenül):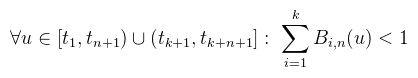


(sőt, ekkor nem csak az n-edfokú szumma ilyen, hanem minden j ≥ m -edfokú is)

Tehát ilyen u-kra nem teljesül az egységosztás tulajdonság, de rögtön látszik is a megoldás, azaz hogy u csak a t_n+1 és t_k+1 knotok között veheti fel az értékét. Az ilyen "rossz" görbék nem érnek el egészen az első és utolsó kontrollpontig, hanem előbb abbamaradnak.

Van azonban még egy javításra szoruló dolog, mégpedig az utolsó felvehető érték (t_k+1) esete. Ezt ugyanis a nulladfokú bázisfüggvény nem kezeli le, márpedig jó lenne, ha a "jó" görbék az utolsó kontrollpontot érintenék. Ezt elég pongyolán lehet garantálni:

Javítás 2: az utolsó érvényes (k-adik) knot span mindkét oldalról zárt.
Tehát t_k+1 beleértendő abba a spanba. Ez felületeknél különösen fontos, mert ha nem veszed bele, akkor a normálvektorban egy ronda törés lesz a felület vége felé.

Most, hogy két hét alatt sikerült megjavítanom ezt a fanbasztikus definíciót, jöjjön a lényeg: hogyan lehet compute shaderrel feltesszellálni egy görbét/felületet (csak egyenletes tesszellációval foglalkozok). A számolásban a legtöbb időt a bázisfüggvények redundáns kiértékelése viszi, viszont ezzel a trükkel ki lehet vinni a ciklusból. Ehhez a bázisfüggvényeket át kell írni a hatványbázisba, és akkor a paperben szereplő képlettel előre kiszámolhatóak a C_i,n,j együtthatók. A hatványbázisban felírt bázisfüggvény így: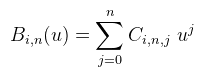


Ezek az együtthatók függetleníthetők u-tól, ugyanis az egész buli a nulladfokú bázisfüggvényre épül, ami viszont adott u-ra csak egy spanon nemnulla. Mivel egy adott spanban csak n+1 kontrollpont van hatással a görbére, elég spanonként ennyi darab tömbben eltárolni az együtthatókat, sőt ezt a workgroup lokális memóriájába lehet pakolni (amíg befér). Még egy jó hír, hogy hatványbázisban baromi könnyű (parciális) deriváltat számolni, ami a normálvektorhoz kell.

Van azonban egy rossz hír is: a GLSL nem tud rekurziót (HLSL sem, OpenCL és CUDA viszont igen, amit nem egészen értek, de mindegy...). Szóval ezt a vidám trükköt először át kell írni iteratívra. Ez könnyen megtehető, hiszen csak C_i,0,0-ból kell kiindulni és minden köztes lépést eltárolni egy (n+1)³ méretű tömbben. Ez szintén elfér a shared memoryban (a szabvány minimum 32 KB-ot követel meg). Ezt pongyolán blossom-nak neveztem el, de nem biztos, hogy ez a pontos felírása a polárformának.

Egy másik GLSL hiányosság az, hogy a makró kifejezéseket nem értékeli ki előre. Szintén egy hibagyanús dolog a többdimenziós tömb, éppen ezért mindent kézzel érdemes kiszámolni. Eddig az AMD-t szidtam, most viszont az nVidia-t fogom ugyanis a user-defined függvényeket rosszul fordítja, ha shared változó a paramétere... Szóval igaz a mondás, miszerint a shader fordító abszolút megbízhatatlan.

Az együtthatók meghatározása után már elég egyszerű a dolog: a work groupon belül elosztva ki kell számolni a görbe pontjait:

• meghatározni u-t
• megkeresni a hozzá tartozó span-t
• elvégezni a szummákat
• normalizálni

Érdekesebb a felület tesszellációja, ugyanis annak normálvektorokat is kell generálni. Amihez parciálisan kell deriválni egy fentinél is rondább képletet. Emlékeztetőül a hányados deriváltja:


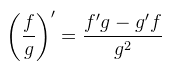
Nos igen...sok sikert kiszámolni. Nem tudom milyen megfontolásból, de egyik implementáció sem számolja ki rendesen (le kell scrollozni a tesszellációs samplehoz), hanem valami olyat csinál, ami csak nekem láthatóan rossz (rosszul deriválják le). Úgyhogy akkor én most megcsinálnám jól. Namost, mivel a képlet baromi hosszú és nem fér ki, valahogyan rövidítenem kell. Legyen az eredeti képlet: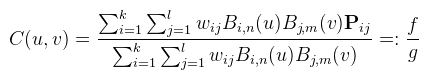


Ezzel a jelöléssel akkor az u szerinti parciális derivált: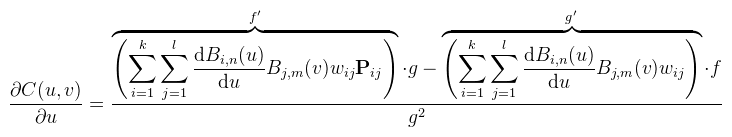


v-re nyilván hasonló. Ezt a négy részt (f, f', g, g') külön ki lehet számolni (ez elsőre nekem sem volt nyilvánvaló), így az egész buli egy (dupla)szummában elvégezhető. Mint említettem, a bázisfüggvényeket könnyű lederiválni; sőt harmadfokúig még valamennyire GPU barát is, mert:


Az így kapott két tangensvektorból a normál már előáll egy vektoriális szorzattal. Harmadfokúnál nagyobbra dot helyett már ciklust kell használni (vagy meggondolni, hogy hogyan lehet mégis dotolni).

Mivel egy NURBS felület két NURBS görbe tenzorszorzata, ezért pongyola módon ugyanazt a görbét tenzorszoroztam önmagával. A felület kontrollpontjait a két görbe kontrollpontjaiból számoltam ki, de általános módszer erre nincs (sajnos). Általában ezeket kézzel szokás megadni.

Néhány megjegyzés: az indexbuffert std430-nak érdemes deklarálni (de ez csak 4.3-tól van), mert az nem paddeli ki 16 bájtra az egyébként érvényes struktúraméretet (uvec2 például érvényes, uint[6] szintén). Egy másik fontos dolog, hogy a glLineWidth megszűnt (van, de nem működik), úgyhogy vonalakat már csak geometry shaderrel lehet rendesen rajzolni.

Ezekkel minimálisan foglalkoztam, de nem implementáltam le, mert soká tart vagy körülményes jól belőni. Igazából elég kevés olyan dolog van grafika témakörben amire értelmesen lehet használni a GPGPU-t, mert a legtöbb algoritmust a fragment shader is meg tudja csinálni.

Postprocess effektek: a workgroup shared memoryjába be lehet cachelni a feldolgozandó texeleket, így összességében sokkal kevesebb olvasásból megvan (pl. gauss blur nagy sugárral).

Ocean rendering: meg akartam csinálni, de soká tart megérteni a komplex számokkal való mókolás miatt. A lényege hogy egy gyakran használt statisztikai alapú hullám modellből gyors Fourier transzformációval kiszámol egy displacement map-ot (minden frameben), amit aztán a víz geometria magasságához és shadeléséhez használ fel. A régi nVidia SDK-ban van implementáció.

Izofelületek/izogörbék: ezt is lehetne "tesszellálni" (marching cubes), de a technológia már adott a direkt raytracelésükhöz (ráadásul baromi gyors és "egyszerű"). A compute shaderes feldolgozás lehetővé teszi az izoérték realtime változtatását sejtésem szerint 512³ méretű skalármezőkig (de az már brutális memória, hacsak nem streameled).

Instant radiosity / reflective shadow map: az RSM a klasszikus shadow map kibővítése úgy, hogy nem csak depth-et, hanem a world space normált és a fluxust is kiírja a shadow mapbe (így olyan lesz mint egy G-buffer). Ennek felhasználása aztán két lehetőségre oszlik:

Bár egy bounce-os GI-t meg tud csinálni, nekem nem tetszik...tetszőleges jelenetet nem lehet vele bevilágítani, mert a RSM-re van limitálva (tehát egy kívülről besütő napfény sosem fog tovább pattogni a kisszobába).

Lightmap/vertex light gyorsabb számolása: a GPU-ról CPU-ra való transfert ki lehet spórolni, ehhez viszont a lightmapnek is és a sample-ket tartalmazó buffernek is olyannak kell lennie ami átfordítható compute shaderes logikára. Lényegesen nem gyorsít rajta, mert a bottleneck nem ez, hanem hogy rengeteg sample-t kell csinálni.

Raytracing: szerintem nem erre való a GPU... Módszerek már vannak (a paper szerint BVH térfelosztással), de a problémákat ezzel nem oldod meg (global illumination-t legalább olyan nehéz belevinni, mint raszterizálással).

Path tracing: erre is van már realtime implementáció, de én szkeptikus vagyok. Maga a módszer Monte Carlo alapú, tehát konvergálnia kell (akkor szép a kép ha nem mozogsz, egyébként mákos).

Cloth simulation: videó nincs is róla, paper viszont van. Érteni kell fizikához.

Ezeknek a (jövőbeli) használatát érdemes meggondolni. Nyilván sokkal több van, de itt csak azokat említem meg, amik szerintem is hasznosak.

ARB_robustness_isolation: a lényege annyi, hogy az alkalmazás által okozott driver reset (crash) esetén más alkalmazások alól nem hal ki a driver. Szkeptikus vagyok, hogy mennyire van/lesz támogatva. Ha tippelni kell akkor azt mondom, hogy nVidia már tudja, AMD még nem is hallott róla, az Apple meg hallani sem akar róla.

ARB_robust_buffer_access_behavior: a bufferekben való túlcímzéseket lenyeli. Ha máshoz nem, crash okának kiderítéséhez jó lehet (de a debug logba is biztos kiír valamit).

ARB_texture_storage: módosíthatatlan textúra. Egy klasszikus textúrának a helyességét rajzolás előtt ellenőrzi a driver, ami fölösleges overhead.

ARB_debug_output: hasznos infókat ír ki a driver (eddig csak nVidia-n láttam működni).

ARB_texture_compression_bptc: támogatja float textúrák tömörítését (HDR képek!!).

ARB_get_program_binary: el lehet kérni a lefordított shader kódot, és később fordítás nélkül be lehet tölteni. Bár az lenne a szép, ha hordozhatóságot is garantálna, azt nem teszi. Mindenesetre sok shader esetén gyorsítja a betöltési időt, sőt nVidia kártyák a disassembly-t is ideadják, ami elég hasznos tud lenni.

A cikkből is látható, hogy értelmesen csak nVidia kártyán sikerült használnom az új extensiönöket. Az említett Radeon 6750M-en nem hajlandó működni az SSBO, csak akkor ha használat után kiolvasom a tartalmát (lehet, hogy ez az első kvantum GPU?). Ez persze nem jelenti azt, hogy az AMD-nek szar kártyái vannak (dehogynem), csak annyit, hogy szar OpenGL drivereket ír. A DirectX drivereik szerencsére stabilabbak, sőt ott van nekik a Mantle is (amit viszont a kutya nem használ).

Tovább rontja az OpenGL helyzetét, hogy Mac-en jó eséllyel a Metal fog propagálódni (ha sikerül leküzdeniük a hardverbeli különbségeket), így gyakorlatilag az nVidia (+Linux) marad az egyetlen aki még életben fogja tartani az OpenGL-t. Sőt, ők annyira életben tartják, hogy a Tegra K1-es mobil GPU már desktop OpenGL 4.4-et is tud.

Néhány mondat debug eszközökről: a gDebugger nem tud compute shadert, sőt le is áll hibával. Mint tudjuk, az AMD CodeXL az örököse, a baj az, hogy semmire nem használható. Az egyetlen eszköz ami marad, az az nVidia nSight. Ez már majdnem olyan jól használható, mint a PIX, bár shadert nem tud debugolni. Arra viszont jó, hogy az SSBO-k tartalmát megnézd, illetve lépésenként lásd a visszajátszásból, hogy mi hogyan rajzolódik.

Kód a szokott helyen. OpenGL 4.3-as kártya kell hozzá. Binárist nem fordítottam, mivel AMD kártyákon elég hektikus, hogy mi történik (szóval mindenki saját felelősségre fordítsa le). Akinek nincs ilyen kártyája, annak töltöttem fel videókat: forward+, NURBS.


Höfö:

• Bojkottálni az AMD-t.
• Bojkottálni a Khronos-t.
• Bojkottálni az OpenCL-t.
• Bojkottálni a B-spline-okat.

Irodalomjegyzék

http://www.crytek.com/download/2014_03_25_CRYENGINE_GDC_... - The Rendering Technology of Ryse (Crytek, 2014)
https://www.khronos.org/assets/uploads/developers/library/... - OpenGL 4.3 Birds Of a Feather (SIGGRAPH 2012)
http://amd-dev.wpengine.netdna-cdn.com/wordpress/media/2012/10/... - DirectCompute by Example (AMD, 2012)
http://bps11.idav.ucdavis.edu/talks/11-towardInteractiveGlobalIllumination... - Interactive Global Illumination (SIGGRAPH, 2011)
http://www.nvidia.com/content/siggraph/Rollin_Oster_OpenGL_CUDA.pdf - OpenGL & CUDA Tessellation (nVidia, 2011)
http://www.dice.se/wp-content/uploads/2014/12/... - DirectX 11 Rendering in Battlefield 3 (DICE, 2011)
http://developer.amd.com/wordpress/media/2012/10/... - Technology Behind AMD's "Leo demo" (AMD, 2010)

http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html - CUDA programming guide (nVidia)
http://www.nvidia.com/content/PDF/kepler/NVIDIA-Kepler-GK110-Architecture-Whitepaper.pdf - Kepler architecture (nVidia)