|
Egy örök kívánság minden 3D alkalmazás részéről, hogy minél valósághűbb legyen a megjelenítés. Mint már korábban említettem, ennek teljes eléréséhez meg kellene oldani a rendering equation-t (vagy ha azt nem is, akkor legalább a radiance equation-t). Bevett gyakorlat ezt ún. lightmap-be kiszámolni (pre-baked global illumination), ami játékok esetében még kivárható folyamat, de a jellegéből adódóan statikus megvilágítási módszer. A rosszabbik tulajdonsága viszont, hogy esetenként kivárhatatlan (pl. nagyobb CAD modelleken). Bár létezik ez az Enlighten nevű cucc, ami valós időben tud lightmapet számolni, de ez is játékokhoz van kitalálva és igen borsos ára van.
TartalomjegyzékInduljunk ki akkor a reflectance/radiance equation, azaz a tükröződési egyenletből. Emlékeztetőül ez egy felületi integrál a felület egy pontja körüli térszögön (előbbit lustaságból elhagyva):
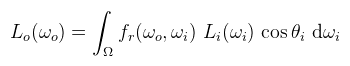
Ahol tehát Lo(ωo) a kimenő iránybeli radiancia (amit tudni szeretnénk), Li(ωi) a bejövő irányból érkező radiancia (fényforrás, vagy egy másik felületről lepattanva), cos θi = dot(n, ωi) azaz a normálvektor és a bejövő irány skaláris szorzata, fr pedig a BRDF, ami kvázi az anyagot határozza meg. Az, hogy Ω konkrétan mekkora térszög, az nincs egyértelműen definiálva (gondoljunk a tökéletes tükröződésre, ahol pontosan egy irányból jön fény). Szerencsére, amikor ambient occlusion-ről beszélünk, akkor a fenti integrál jelentősen egyszerűsödik az alábbi megszorítások által:
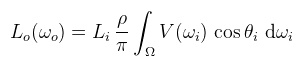
Mivel a beérkező radiancia konstans, az egyenlet elvesztette a rekurzív jellegét, de sajnos ez a hivatalos definíció. Természetesen nem így kellene működnie, ezért a pattogások szimulálásához alkalmazni szoktak rá valamilyen függvényt; ekkor ambient obscurance a neve (jegyezzük meg, mert az irodalmak olvasásakor fontos, hogy mit is implementálnak!). Kezdésképpen nézzük meg, hogy mit tudunk elérni a klasszikus Monte Carlo integrálással. Tulajdonképpen ez nem path tracer, hiszen nem pattogunk egynél tovább. A szokásos technikákat viszont nyugodt szívvel alkalmazhatjuk. Írjuk fel a felületi integrált Monte Carlo közelítéssel (Li = 1-et feltételezve):
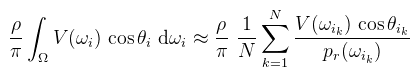
Amit szerencsére még tovább tudunk egyszerűsíteni, hiszen a Lambert BRDF-hez már ismerünk egy gyorsan konvergáló mintavételezési stratégiát: 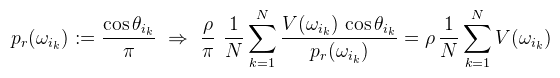
Ezen sűrűségfüggvényhez ωik-t az alábbi kóddal kell megválasztani a felületi normálvektor, illetve valamilyen ξ1 és ξ2 véletlenszerű értékek alapján: CODE
vec3 CosineSample(vec3 n, float xi1, float xi2)
{
float phi = 2 * M_PI * xi1;
float costheta = sqrt(1 - xi2); // mert P(θ) = 1 - cos2 θ
float sintheta = sqrt(1 - costheta * costheta); // mert sin2 x + cos2 x = 1
vec3 h = vec3(sintheta * cos(phi), sintheta * sin(phi), costheta);
return TransformToHemisphere(h, n);
}
Innentől kezdve a path tracer hihetetlenül egyszerű, ugyanis a fenti (egy pixelre való) szummázás egy lépése a felület egy adott x pontján az alábbi kód: CODE
vec3 SampleAmbientOcclusion(vec3 x, vec3 n)
{
float xi1 = Random(gl_FragCoord, time);
float xi2 = Random(gl_FragCoord, time);
vec3 omega_i_k = CosineSample(n, xi1, xi2); // ωik
float V = FindIntersection(x, omega_i_k); // 1 ha eltalált valamit, egyébként 0
return vec3(V);
}
Ez tehát a szummázás egy darab lépése, ami a gyakorlatban egy darab textúra kitöltését jelenti. A lépésekből előáll egy textúra sorozat, amiket már csak átlagolni kell. A memóriafelhasználás javításának érdekében elég két textúra között pingpongozni, az előzőt lineárisan (exponenciálisan!) interpolálva az aktuálisan kiszámolthoz: CODE
uniform sampler2D prevIteration;
uniform float k;
void main()
{
vec3 surfpoint, surfnormal;
// ...
vec3 prev = texelFetch(prevIteration, ivec2(gl_FragCoord.xy), 0).rgb;
vec3 curr = SampleAmbientOcclusion(surfpoint, surfnormal);
float d = 1.0 / k;
gl_FragColor0.rgb = mix(prev, curr, d);
}
És ezzel készen is van az (egyelőre) pattogások nélküli path tracer. A számolás egyszerűsége miatt igen gyorsan konvergál, gyakorlatilag néhány ezer iteráció után már teljesen szép képet ad. Nézzünk meg néhányat: 
Vegyük észre, hogy az objektumoknak szürkés árnyalata van, holott szinte minden irányból kapnak fényt. Na persze, kivéve alulról, ahol is egy végtelen féltér van, így onnan egyáltalán nem érkezik fény; ez okozza a szürkeséget, mégpedig amiatt, hogy tetszőlegesen messze levő irányban is talál vele metszést az algoritmus (far field occlusion). Ha ez a "padló" nem lenne ott, akkor többnyire fehér lenne minden, kivéve ahol elég közel van egymáshoz két objektum (near field occlusion). A feladat valami hasonlót csinálni postprocess lépésekben. A fentiekből következik, hogy screen space-ben csak a near field occlusion-t tudjuk értelmesen közelíteni, hiszen a kamerán kívüli objektumokról semmilyen információnk nincs. Az egyetlen adat, ami rendelkezésre áll, az a depth buffer (illetve a normálvektorok).
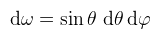
Aminek értelmében - és mivel a térszög egy félgömb - a fenti felületi integrált felírhatjuk (dupla) Riemann integrálként: 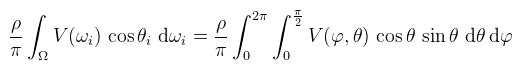
(megj.: azaz egy negyedkört megpörgetek a normálvektor körül, így állítva elő a félgömböt) Most jön egy nagyszerű felfedezés: a depth buffer tekinthető magasságmezőnek (ez persze általában nem igaz, merthogy nem folytonos...), tehát minden olyan irány, ami emiatt takarásban van nem releváns nekünk. Úgy is lehetne mondani, hogy egy kiválasztott pont normálvektorának környezetében minden φ-re tudok találni egy olyan minimális ún. horizont szöget, hogy azon túl már V(φ, θ) == 0 feltehető. Így ha csak addig végzem az integrálást, akkor V-re nincs szükség a képletben. Na de akkor a belső integrált megoldhatom analitikusan! Először nézzünk egy ábrát, hogy miről is beszélek: 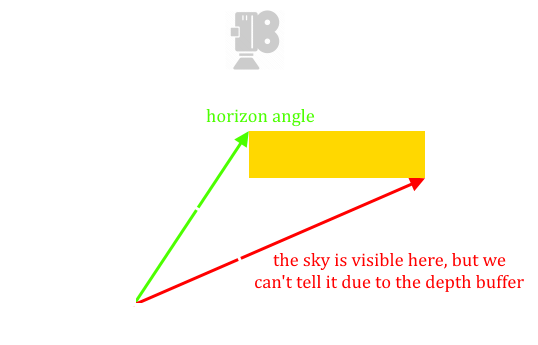
A negyedkörben besatíroztam azokat a részeket, ahol V(φ, θ) == 1, de az alsót nem tudjuk detektálni, mert a depth buffer nem hordoz elég információt hozzá. Így tehát ilyen esetekkel nem kell foglalkoznunk: feltehetjük, hogy az ábrán zölddel jelölt horizont szögön túl az integrandus végig nulla. Jelöljük ezt a szöget h-val és számoljuk ki a belső integrált: 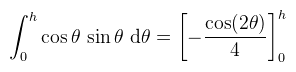
Most persze mindenkit elöntenek az örömkönnyek, hogy milyen egyszerűen megoldottuk a feladatot, hiszen egy adott pixelre választunk φk irányokat, megkeressük a hozzá tartozó hk-t, kiértékeljük a képletet, majd ezeket összeadjuk... Bár ilyen egyszerű lenne az élet... A fenti ábrán ugyanis szándékosan nem írtam ki, hogy mi a fehér vektor. A kontextus alapján azt mondanánk, hogy a normálvektor, de ne felejtsük el, hogy az bármilyen irányba nézhet, tehát egy screen space-ben való keresés szinte mindig rossz horizont szöget fog találni! 
Ha ránézünk a bal oldali ábrára, akkor látható, hogy adott φ-re a horizont szöget nem egy egyenes mentén kellene keresni, hanem egy ív mentén. Ha viszont a normálvektor helyett a nézeti vektort válasszuk az integrálás tengelyének, akkor az ívekből egyenesek lesznek (mintha felülről néznénk egy gömböt). De vajon megtehető-e ez, és ha igen, akkor hogyan kell módosítani a képletet? Az első kérdésre az a válasz, hogy természetesen megtehető, hiszen a tengely megváltoztatása csak annyit jelent, hogy a 0 (mint szög/térszög) máshová kerül a félkörön/félgömbön belül. Ez magával rántja persze az integrálás tartományának megváltozását is (ami magával hozhatja azt is, hogy a szinusz többé nem érvényes; az abszolútértékét kell venni!). A második kérdés megválaszolásához először meg kell érteni, hogy az integrandusban mi az a cos θ. A jelölés félrevezető, ugyanis az eredeti képletben a normálvektor és az ahhoz tartozó félgömbből vett ωi skaláris szorzataként szerepel. Az valóban igaz, hogy ha az integrálás tengelye a normálvektor, akkor ez egybeesik cos θ-val. Ha azonban megváltoztatom a tengelyt, akkor a normálvektortól való eltérést annak megfelelően kell kompenzálnom. Ami annyira nem is triviális dolog, hiszen most a normálvektor nincs is benne a φ-hez tartozó félkör síkjában! Szerencsére bizonyítható, hogy a levetített normálvektorral (ñ) is elvégezhető a számolás (amit majd szintén kompenzálni kell). Nézzünk először egy ábrát: 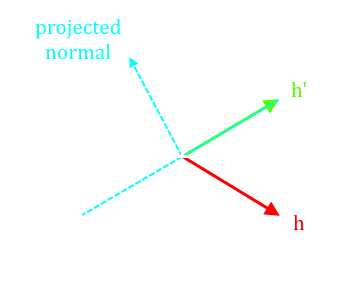
A képen azt látjuk, hogy a horizont szöget (h) most már a nézeti vektorhoz képest keresem, aminek az a következménye, hogy nem feltétlenül esik bele a normálvektor félkörébe. Az eredeti formula viszont ezt nem engedi meg, ezért az ilyen szélsőséges eseteket vissza kell szorítani az eredeti félkörbe (így lesz h'). Ha ezt nem tenném meg, akkor az integrálás túllendülne a maximális értékén, azaz túlvilágosodást okozna. Az ábrán szereplő γ a nézeti vektor és a félkörre vetített normálvektor által bezárt előjeles szög (ez különösen fontos, később megmutatom hogyan kell kiszámolni). Ekkor az integrált a következőre kell módosítani: 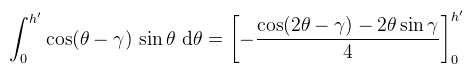
Amit most már kiszámolhatunk, és jelöljük mondjuk â(φ)-vel. A normálvektor vetítését úgy kell kompenzálni, hogy az eredményt megszorozzuk ñ hosszával (bizonyítható, de nem vezetem le): 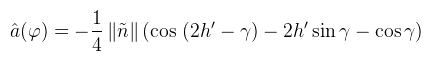
Csak hogy világos legyen: h' és ñ kiszámolása függ φ-től, de nem akartam függvényként kiírni. Ez tehát a belső integrál; a frissen szerzett tudással felvértezve írjuk fel a külső integrált is és rögtön alakítsuk át Monte Carlo formába: 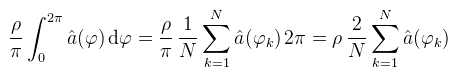
Valóban, ide teljesen jó az egyenletes eloszlás, azaz pr = 1 / 2π (nem mindenki ért velem egyet, úgyhogy halványan írtam ide...). Ezzel gyakorlatilag készen is vagyunk; N növelésével lehet javítani a közelítés pontosságán. Hasonlítsuk össze a most kiszámolt GTAO-t a fentebb írt path tracer-el (hogy tisztességes legyen, a padlót kivettem): 
Ugye mindenki látja a különbséget, ami abból adódik amit fent lerajzoltam? A hátsó gömbök oldalról is kapnak fényt, de azt a depth buffer-ből nem tudjuk meghatározni, így ott a GTAO sötétebb. A többi példajelenetet egyelőre nem mutatom meg, mert (megj.: azt, hogy "ronda" úgy kell érteni, hogy millióegy dolgot nem vettem még figyelembe; speciel a gömb annyira tökéletes konstrukció, hogy nagyon kevés artifact látszik rajta) Az elméleti háttér ismeretében kezdjük el akkor megírni a kódot, ami a fenti képet előállítja. Az első kérdés, amit le kell tisztázni, hogy milyen normálvektorokat használjunk? Az interpolált normálvektorok ugyanis valótlan eredményt adhatnak. A legtöbb irodalom a depth buffer-ből visszafejti az interpolálatlan normálokat és azzal számol. Az viszont ilyen "baltával faragott" hatást kelt, amit mindenféle hackeléssel kényszerülnek eltüntetni...
CODE
#version 150
#define NUM_DIRECTIONS 32 // ennyi negyedkörre bontom a félgömböt
#define NUM_STEPS 16 // ennyi lépésben keresem a horizontot
#define RADIUS 2.0 // 2 méteres környezetben
uniform sampler2D gbufferDepth;
uniform sampler2D gbufferNormals;
void main()
{
ivec2 loc = ivec2(gl_FragCoord.xy);
vec3 vpos = GetViewPosition(gl_FragCoord.xy); // mindenki el tudja képzelni
vec3 vnorm = texelFetch(gbufferNormals, loc, 0).rgb; // view space-beli (!) normálvektor
vec3 vdir = normalize(-vpos.xyz); // nézeti vektor
float ao = 0.0;
float m2pixel = 0.5 * (screenheight / (2.0 * tan(fov * 0.5))); // ezt CPU oldalon számold
float radius = (RADIUS * m2pixel) / vpos.z; // max ilyen messze keresek
float stepsize = radius / NUM_STEPS; // ennyit ugrok egy lépéssel
for( int k = 0; k < NUM_DIRECTIONS; ++k ) {
float phi = k * (M_2PI / NUM_DIRECTIONS); // ϕk
float h = -1.0;
vec3 dir = vec3(cos(phi), sin(phi), 0.0);
//TODO: horizont szög megkeresése
//TODO: vetített normál kiszámolása
//TODO: h' kiszámolása
//TODO: integrálás
}
ao = (2.0 * ao) / NUM_DIRECTIONS;
my_FragColor0 = vec4(ao, ao, ao, 1.0);
}
Amit itt leírtam az meglehetősen különbözik a kódmelléklettől (az érthetőség érdekében), mert ahogy majd később látni fogjuk teljesítmény/minőség szempontból optimálisabb, ha negyedkör helyett félkörön számolok, ezáltal két horizont szög között végezve el az integrálást. Ezt az optimalizálással foglalkozó bekezdésben említem meg. Előtte viszont nézzük meg a //TODO:-val jelölt részeket.
Kezdjük ezzel, mert később sok minden fog ráépülni. Ha a szöget minimalizálni szeretném, az ekvivalens azzal, hogy a koszinuszát maximalizálom (amit könnyen ki lehet számolni). A kódban szereplő dir irányban lépkedek tehát és vizsgálom a megfelelő view space-beli pontot. Hogy a keresés cache barát legyen, a makróként megadott world space-beli sugarat átszámoltam pixelbe (a fenti radius).
CODE
float currstep = 1.0;
for( int j = 0; j < NUM_STEPS; ++j ) {
vec2 offset = round(dir.xy * currstep);
vec3 sample = GetViewPosition(gl_FragCoord.xy + offset);
h = max(h, dot(normalize(sample - vpos), vdir));
currstep += stepsize;
}
h = acos(h);
Gondolom nem kell különösebb magyarázat; tudjuk hogy a skaláris szorzás mit ad meg, vizualizációhoz pedig ott a korábbi rajz. Ezzel a kereséssel annyi baj van csak, hogy nem foglalkozik azzal, hogy milyen messze van a minta, és olyat is felhasznál, ami akár kilométerekre van az aktuális ponttól. Tisztázzunk le valamit: az ambient occlusion definíciójában szó nincs távolságról. Csak az érdekli, hogy az égbolt mekkora térszög alól látszik. Teljesen mindegy neki tehát, hogy egy felület 2 centire vagy 2 kilométerre van; az általa bezárt térszögből nem érkezik fény (mégegyszer, ez a far field occlusion). Megbeszéltük viszont, hogy screen space-ben csak a near field occlusion-al tudunk foglalkozni, azaz a fenti kód értelmében egy távol levő objektumon is meg fog jelenni egy közeli által kiváltott árnyék, ami lássuk be, hogy elég idiótán néz ki. Tehát igen, sajnos figyelembe kell venni a távolságot. Egy lehetséges megoldás az alábbi: CODE
#define FALLOFF_START 0.5
vec3 ws = sample - vpos;
float dist = length(ws);
float cosh = dot(normalize(ws), vdir);
float falloff = clamp((dist - FALLOFF_START) / (RADIUS - FALLOFF_START), 0.0, 1.0)
h = max(h, cosh - 2.0 * falloff);
A kettővel szorzás azért kell, mert a tartományváltás miatt a normálvektorral bezárt szög simán lehet nagyobb, mint ±π/2, tehát ha ki akarok hajítani egy mintát, akkor számolás eredménye negatív kell legyen. Bár a látható hibák nagy részét megoldja, ez sem tökéletes. Lehet próbálkozni más függvényekkel is (pl. exp(-dist)), vagy elolvasni a Pixar jegyzetét. Ahogy mondtam, a nézeti vektor körüli integrálás miatt a normálvektor nem esik bele a φ által meghatározott félkörbe, ezért azt le kell oda vetíteni. Ez megtehető úgy, hogy kiszámoljuk a félkör síkjának normálvektorát (mivel dir és vdir benne vannak, a kettő vektoriális szorzata ezt meg is adja), onnantól pedig alkalmazható a klasszikus vektor→sík vetítés:
CODE
// vetített normál kiszámolása
vec3 bitangent = normalize(cross(dir, vdir));
vec3 nx = vnorm - bitangent * dot(vnorm, bitangent);
Ugye mindenki látja, hogy szándékosan nem normalizáltam le? Merthogy megbeszéltük, hogy a normájára (hosszára) szükség lesz később (aminek kiszámolását gondolom nem kell részletezni). Fontosabb viszont a γ jelű előjeles szög kiszámolása. Ha simán skaláris szorzatot számolnék, akkor ugyanis nem lehetne eldönteni az előjelet (cos(x) == cos(-x)). Megtehető viszont az, hogy teljesen ortogonalizálom a bázist (vdir, bitangent, tangent) és akkor mérhetünk a félkör aljától (és ez az ÉN ötletem!!!): CODE
// γ kiszámolása
vec3 tangent = cross(vdir, bitangent);
float norm_nx = length(nx);
float gamma = acos(dot(nx, tangent) / norm_nx) - M_HALF_PI;
Szintén megbeszéltük, hogy a horizont szög nem feltétlenül esik bele a normálvektor félkörébe, úgyhogy vissza kell oda szorítani: CODE
// h' kiszámolása
h = gamma + min(h - gamma, M_HALF_PI);
És egyetlen dolog van még hátra: lekódolni a fenti â(φ)-re vonatkozó képletet: CODE
float cosgamma = dot(nx, vdir) / norm_nx;
// integrálás
ao += norm_nx * 0.25 * (h * 2.0 * sin(gamma) + cosgamma - cos(2.0 * h - gamma));
Ezzel egyelőre el van intézve a probléma, viszont brute-force megoldás, szóval a minőség növelésével egyenes arányban lassul. A továbbiakban az lesz a feladat, hogy a külső ciklust elhagyva végezzük el a Monte Carlo integrálást. A path tracer-ben azt csináltuk, hogy minden iterációs lépésben, sőt azon belül is minden pixelre egy véletlenszerű irányban számoltuk ki az occlusion-t, így "sok kicsi sokra megy" alapon az átlag egy idő után kihozta a kívánt eredményt. Persze ha megmozdítom a kamerát, akkor elölről kezdi, ami annyira nem néz ki jól egy játékban...
A fenti kódból látszik, hogy két olyan dolog van, amiből lehetőleg minél többet szeretnénk: a negyedkörök száma, illetve a horizont keresés lépéseinek száma. Csináljuk azt, hogy egy pixelre mindössze két darab negyedkört számolunk ki (pontosabban egy félkört): CODE
uniform sampler2D noise; // 4x4-es randomizáló textúra
vec2 rndvalues = texelFetch(noise, ivec2(gl_FragCoord.xy) % 4, 0).rg;
float phi = rndvalues.x * M_PI;
float currstep = 1.0 + rndvalues.y * (stepsize - 1.0);
vec3 dir = vec3(cos(phi), sin(phi), 0.0);
float ao = CalculateAO(dir) + CalculateAO(-dir);
Sőt, akár négyet is lehetne, ha a hardver erős. Na de hogyan válasszuk meg a kernelt? A GTAO egyik ötlete, hogy a 4x4-es textúrában el lehet osztani 16 különböző szöget úgy, hogy bármely sort vagy oszlopot kiválasztva egy teljes kört kapunk. A horizont keresés kiindulólépésének véletlenszerűsítése szintén ehhez igazítható (bár kevésbé látványos). A randomizációs textúra így néz ki (red/green channel): 
A shaderben ezek értelemszerűen [0, 1]-beli értékek. Az előállításuk megtalálható az Activision prezentációjában (vagy egyszerűen kimásolod a képről...). Ne felejtsük el azonban, hogy az integrálás tartományának megváltoztatása miatt az eredmény már nem esik bele a [0, 1] intervallumba, úgyhogy ezzel a megoldással legalább float16 textúrába kell írni a GTAO-t (vagy leosztod 1.8-al, csak aztán ne felejtsd el visszaszorozni). A szummázást tehát elkésleltettük, viszont az eredmény intervallumának megváltozása miatt kötelező rekonstruálni, ami a megválasztott 4x4-es kernel miatt egy ugyanekkora elmosást jelent. Ezt bár meg lehet csinálni egyszerű átlagolással is, nem szeretnék átmosni egymástól távol levő objektumokon (tehát az objektumok széleinél meg akarom tartani az élességet).
CODE
float BilateralWeight(vec2 uv, float d0)
{
float d = texture(gbufferDepth, uv).r;
return max(0.0, 0.1 - abs(d - d0)) * 30.0;
}
Tulajdonképpen nem is ez az érdekes; csinálhatsz mezei átlagolást is. Az viszont fontos, hogy a képet 2 pixellel eltoljad, mert akkor fog egybeesni a jelenettel. 
Ha a kapott kép összességében nem fehér túnusú, vagy nézetfüggően olyan, akkor valamit elrontottál. Érdemes először a GTAO-t rendesen megcsinálni (pixelenként elvégezve a Monte Carlo-t) és utána foglalkozni ezzel. Ha túl mosottasnak találod a képet, akkor használj 2x2-es kernelt és/vagy buheráld meg a bilaterális szűrőt. Térjünk át most a módszer időbeli konvergáltatására (temporal reprojection). Egyszerű megoldásként meg lehet azt csinálni, hogy ha megállsz a kamerával, akkor N frame-en keresztül megpörgeted a kernelt, az eredményeket pedig átlagolod. Ez a megoldás viszont csak statikus jelenetekre jó; ha bármi mozgás van, akkor értelmét veszti.
Disocclusion akkor történik, amikor olyasmi válik láthatóvá az aktuális frame-ben, ami az előzőben még nem volt ott. Ennek detektálását legjobban az említett TSSAO dolgozat írja le: reverse reprojection-el megkeresem, hogy az aktuális pixelhez tartozó world space-beli pont hová vetítődött az előző frame-ben, és ezt az új pixelt felhasználva az előző frame depth buffer-éből visszafejtem az akkori (szintén world space-beli) pozíciót. Ha a kapott két pozíció között elég nagy a távolság, akkor ott disocclusion történt és a konvergenciát újra kell indítani. Nézzünk egy rövid kódot: CODE
uniform sampler2D historyBuffer;
uniform sampler2D currIteration;
uniform sampler2D prevDepthBuffer;
uniform sampler2D currDepthBuffer;
// visszavetítem world space-be az aktuális kamera mátrixxal
float currdepth = texture(currDepthBuffer, tex).r;
vec3 currpos = GetWorldPosition(currdepth, tex * 2.0 - 1.0, matCurrViewInv);
// reverse reprojection az előző frame screen space-ébe
vec3 tempspos = GetScreenPosition(currpos, matPrevView, matProj);
// kiderítem, hogy akkor mi volt éppen a world space pozíció
float prevdepth = texture(prevDepthBuffer, tempspos.xy * 0.5 + 0.5).r;
vec3 prevpos = GetWorldPosition(prevdepth, tempspos.xy, matPrevViewInv);
// ha a két pont távolságnégyzete elég nagy, akkor disocclusion történt
float dist2 = dot(currpos - prevpos, currpos - prevpos);
// ...
A kód lényegi része ez az algoritmus. Ha nem történt disocclusion, akkor növelem pixelhez tartozó számlálót (szintén a rendertargetben tárolva), illetve az aktuális GTAO eredményt hozzáblendelem a history-hoz és az lesz az új history. Értelemszerűen ezt a gyakran használt ping-pong stílusban kell megcsinálni, tehát két darab RG8 textúra csereberélődik minden frame-ben. Optimalizálásként elég csak a prevdepth-ig számolni, és az abs(1 - currdepth / prevdepth) értéket hasonlítani valami epszilonhoz. Azt mindenképpen el kell mondanom, hogy ez a fajta módszer csak statikus jelenetekre jó. Ha ugyanis bármilyen mozgó objektum van, akkor az nem jelent disocclusion-t, viszont az AO csíkot fog hagyni maga után. Ilyenkor már szükség van egy ún. velocity buffer-re, ami az előző és az aktuális frame NDC koordinátáinak különbsége. Sőt, ebben az esetben kell egy újabb algoritmus, amit neighbourhood clamping-nak hívnak és arról szól, hogy az aktuális GTAO eredmény 3x3-as környezetében megkeresed a min/max értékeket és azokra szorítod le a korábbi (history) értéket. Ekkor már inkább az exponential smoothing-ot célszerű választani, bővebben ld. Filmic SMAA. Néhány mondat még arról, hogy milyen hibái vannak a módszernek. Ha a disocclusion detektálásához használt toleranciaküszöb viszonylag kicsi, akkor gyakrabban kezdi újra a konvergenciát, ettől "flicker"-el mozgás közben. Ezen low pass filter-ekkel még lehet segíteni. Viszont egy érdekesebb probléma, hogy az eredmény helyenként "hullámzik". Ezt lehet indokolni több dologgal is, de szerintem azért van, mert a GTAO hülyeségeiből indultam ki és arra alkalmaztam a TSSAO módszerét. Ha normal mapping-et is beleveszel az AO-ba, akkor az csak ront a helyzeten (hiszen egy nem létező geometriára számoltál AO-t, de a disocclusion detection az eredetire vonatkozik). Ezt a hullámzást nem sikerült kiküszöbölnöm, úgyhogy höfö. Először is bebizonyítom, hogy a fent leírt számolásom ekvivalens a GTAO szerzői által megadottal. Ehhez nézzük meg az ő formalizációjukat:
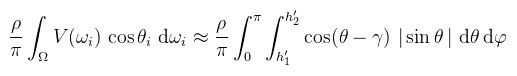
Tehát ahogy korábban említettem, az eredeti dolgozat félkörökön dolgozik, két horizont szöget (h1' ≤ 0 és h2' ≥ 0) kiszámolva és azok között végezve az integrálást. A szinusz viszont a [-π/2, 0] intervallumban negatív eredményt ad, ami miatt az integrálás eredménye is ott negatív. Csakhogy az úgy helytelen, emiatt a szerzők abszolútértékbe tették. Én azért nem ezt a fajta formalizálást használtam, mert így a belső integrál integrandusának nincs primitívfüggvénye, ami sok olvasót összezavarhat. Azt lehet csak tenni, hogy a Riemann integrál additivitását felhasználva két részre bontjuk: 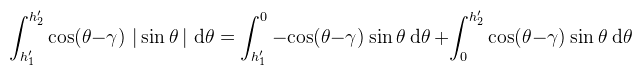
Amire már lehet alkalmazni a Newton-Leibniz szabályt, így az alábbit kapjuk: 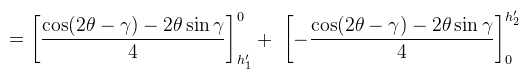
Az eredmény pedig: 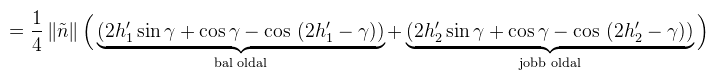
Oké, de hogyan lesz ez ekvivalens azzal, amit én csináltam? Ugyebár két negyedkörre számolom ki az integrált, majd a kapott eredményeket összeadom. Azaz két külön γ-t számolok ki, legyenek ezek γ1 és γ2, amikre persze teljesül, hogy γ1 = π - γ2. Na de: 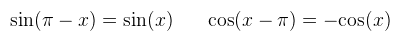
Ha ezeket alkalmazzuk az általam adott módszerre, akkor könnyen látható, hogy pontosan ugyanazt fogjuk kapni, amit az imént leírtam. □ A lényeg tehát annyi, hogy első optimalizációként elég egyszer kiszámolni γ-t, a horizont szögeket pedig a [-π/2, π/2] intervallumban keresni. Ehhez a következőre kell módosítani a normálvektor félkörébe való visszaszorítást: CODE
// h1' és h2' kiszámolása
h1 = gamma + max(-h1 - gamma, -M_HALF_PI);
h2 = gamma + min(h2 - gamma, M_HALF_PI);
A második optimalizáció egy további trigonometrikus azonosságot használ ki, amivel megspórolunk egy szinuszt (ez szintén az én észrevételem!!!): CODE
float cosxi = dot(nx, tangent) / norm_nx; // xi = gamma + π/2
float gamma = acos(cosxi) - M_HALF_PI;
float singamma = -cosxi; // mert cos(x + π/2) = -sin(x)
És ha ez még mindig nem lenne elég, akkor a szerzők mutatnak példakódot gyors acos és sqrt számolásra. (megj.: metálban van külön precise:: és fast:: névtér, így ott nincs szükség külön trükkökre) Először is elmondanám, hogy ez egy több szempontból is nehéz implementáció volt, ugyanis az irodalmak pongyolán, sőt hibásan írnak le rengeteg dolgot. Felvettem a kapcsolatot a szerzőkkel és hónapokig leveleztem velük, mire a saját észrevételeimet és javaslataimat elkezdték komolyan venni és ezáltal érdemben segíteni. Természetesen mindannyiukat köszönet illeti.

Elfogadható, főleg ha figyelembe vesszük, hogy a jobb oldali kép előállítása ~200-szor gyorsabb. Mint mondtam, a mosottságon lehet javítani kisebb randomizáló kernellel, vagy a lépések más (jobb) sorrendben történő elvégzésével. A módszerhez alkalmazni szokás még egy ún. guard band-ot, hogy ne tűnjön el hirtelen az AO, amikor az occluder kikerül a látószögből. Ez csak annyit jelent, hogy pl. nagyobb felbontásban renderelsz, az utolsó lépésben pedig kivágod belőle az eredetit. Egy másik kérdés, ami foglalkoztatott, hogy mobil GPU-kon alkalmazható-e a módszer. Jelentem igen, sőt a 2732x2040 felbontású iPad Pro-mon 15-20 fps-en fut (optimalizálatlanul, teljes felbontásban!). Ez rendkívüli teljesítmény! Kód a szokott helyen, videó pedig itt. Höfö:
Irodalomjegyzék https://research.activision.com/.../Practical-Real-... - Practical Realtime Strategies for Accurate Indirect Occlusion (Activision, 2016) https://research.activision.com/.../Filmic-SMAA-Sharp-Morphological-... - Filmic SMAA (Activision, 2016) https://users.cg.tuwien.ac.at/matt/tssao/ssao.pdf - High Quality SSAO using Temporal Coherence (Oliver Mattausch, 2009) http://frictionalgames.blogspot.hu/2014/01/tech-feature-ssao-and-... - SSAO and Temporal Blur (Frictional Games, 2014) https://developer.nvidia.com/.../GDC12_Bavoil_Stable_SSAO_In_BF3_With_STF.pdf - Stable SSAO in Battlefield 3 (nVidia, 2012) |
